
| A. | $8\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{5}$ |
分析 通过直线l转化为直线系,求出直线恒过的定点,说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,由勾股定理即可得到最短弦长.
解答  解:由(2m+1)x+(m+1)y-7m-4=0,m∈R得:(x+y-4)+m(2x+y-7)=0,
解:由(2m+1)x+(m+1)y-7m-4=0,m∈R得:(x+y-4)+m(2x+y-7)=0,
∵m∈R,
∴$\left\{\begin{array}{l}{x+y-4=0}\\{2x+y-7=0}\end{array}\right.$,得x=3,y=1,
故l恒过定点D(3,1).
因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
圆心C(1,2),半径为5,|CD|=$\sqrt{5}$,
当截得的弦长最小时,l⊥CD,最短的弦长是2$\sqrt{25-5}$=4$\sqrt{5}$.
故选B.
点评 本题考查直线系方程的应用,考查直线与圆的位置关系,考查平面几何知识的运用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
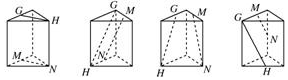
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2P |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4,8,6 | B. | 6,8,4 | C. | 6,10,2 | D. | 8,4,6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0 | B. | $0<a<\sqrt{2}$ | C. | 0<a<2 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
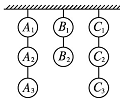 在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?
在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com