
| A. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ | B. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
分析 由题意画出图形,利用向量加法的三角形法则得$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$,转化为$\overrightarrow{AB}$及$\overrightarrow{AD}$得答案.
解答 解:如图,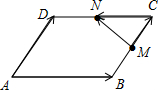
∵$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,且M、N分别是BC、CD的中点,
∴$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$=$\frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}=-\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$.
故选:B.
点评 本题考查平面向量的基本定理,考查了向量加法的三角形法则,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4,8,6 | B. | 6,8,4 | C. | 6,10,2 | D. | 8,4,6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2048 | B. | 2049 | C. | 2050 | D. | 2051 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
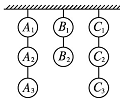 在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?
在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
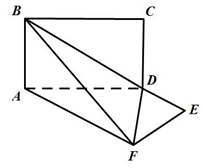 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com