
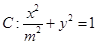 (常数
(常数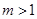 ),点
),点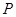 是
是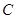 上的动点,
上的动点,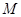 是右顶点,定点
是右顶点,定点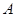 的坐标为
的坐标为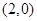 。
。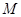 与
与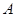 重合,求
重合,求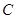 的焦点坐标;
的焦点坐标;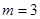 ,求
,求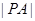 的最大值与最小值;
的最大值与最小值;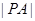 的最小值为
的最小值为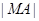 ,求
,求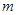 的取值范围。
的取值范围。科目:高中数学 来源:不详 题型:解答题
 及点
及点 ,在
,在 上任取一点
上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 到线段
到线段 的距离,记作
的距离,记作 。
。 到线段
到线段 的距离
的距离 ;
; 是长为2的线段,求点集
是长为2的线段,求点集 所表示图形的面积;
所表示图形的面积;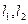 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
,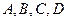 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 本小题满分12分)
本小题满分12分) 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为 的直线
的直线 与C交于A、B两点,点P满足
与C交于A、B两点,点P满足

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
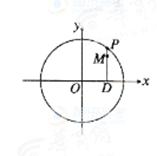
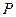 是圆珠笔
是圆珠笔 上的动点,点D是
上的动点,点D是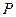 在
在 轴上的投影,M为
轴上的投影,M为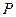 D上一点,且
D上一点,且
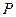 的在圆上运动时,求点M的轨迹C的方程;
的在圆上运动时,求点M的轨迹C的方程; 的直线被C所截线段的长度。
的直线被C所截线段的长度。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com