
分析 抓住两个关键点,一是直线过(0,1);一是直线与圆相切,分别求出m的值,即可确定出直线与圆在第一象限内有两个不同的交点时a的范围.
解答 解:分两种情况:当直线$x+\sqrt{3}y=a$过(0,1)时,将x=0,y=1代入得:a=$\sqrt{3}$;
当直线$x+\sqrt{3}y=a$与圆 x2+y2=1相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{1+3}}$=r=1,
x2+y2=1相切时,圆心到直线的距离d=$\frac{|a|}{\sqrt{1+3}}$=r=1,
解得:a=2或-2(舍去),
则直线与圆在第一象限内有两个不同的交点时,实数a的取值范围是($\sqrt{3}$,2).
故答案为($\sqrt{3}$,2).
点评 此题考查了直线与圆的位置关系,解题的关键是抓住两个关键点,一是直线过(0,1);一是直线与圆相切.


科目:高中数学 来源: 题型:选择题
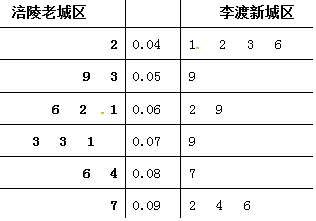
| A. | 李渡新城区 | B. | 涪陵老城区 | ||
| C. | 李渡新城区、涪陵老城区相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-1,+∞) | C. | (-∞,-1] | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2a}{b}$ | B. | 2a-b | C. | a2-b | D. | $\frac{a^2}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com