
分析 根据诱导公式、三角函数的单调性,判断各个选项是否正确,从而得出结论.
解答 解:①sin $\frac{π}{6}$=sin$\frac{7π}{6}$,错误,因为sin$\frac{7π}{6}$=-sin$\frac{π}{6}$=-$\frac{1}{2}$;
根据诱导共式,②cos(-$\frac{π}{4}$)=cos$\frac{π}{4}$正确;
根据y=tanx在(0,$\frac{π}{2}$)上单调递增,故③tan$\frac{π}{8}$>tan$\frac{3π}{8}$错误;
根据y=sinx在($\frac{π}{2}$,π) 上单调递减,可得④sin$\frac{3π}{5}$>sin $\frac{4π}{5}$正确.
故答案为:②④.
点评 本题主要考查诱导公式、三角函数的单调性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)>f(x2) | B. | f(x1)<f(x2) | C. | f(x1)=f(x2) | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
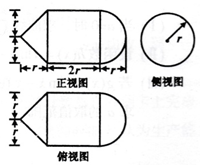
| A. | 4π | B. | 2π | C. | $\frac{11}{3}$π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-1 | B. | a≥-1 | C. | a≤1 | D. | a≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com