考点:等差数列的通项公式,二次函数的性质,等差数列的前n项和
专题:点列、递归数列与数学归纳法
分析:(1)根据对称轴,得到2n+1an+1-2nan=2,继而得到{2nan}是以2为首项,以2公差的等差数列,根据等差数列的通项公式求出an,
(2)利用错位相加法求出数列的前n项和为Sn,并利用函数的思想,得到Sn<3成立的n值.
解答:
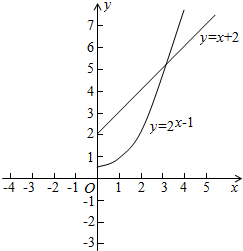
证明:(1)∵二次函数f(x)=
a
n•x
2+(2
-n-a
n+1)•x的对称轴为x=
.
∴
=
,
∴2
n+1a
n+1-2
na
n=2,
∵a
1=1,
∴2a
1=2,
∴{2
na
n}是以2为首项,以2公差的等差数列,
∴2
na
n=2+2(n-1)=2n,
∴a
n=
=n
•()n-1.
(2)∵S
n=a
1+a
2+…+a
n=1×
+2×
+3×
+…+n
•()n-1,
∴
S
n=1×
+2×
+3×
+…+n
•,
两式相减得,
S
n=
+
+
+
+…+
-n
•=
-n
•=2-
•-n
•,
∴S
n=4-
,
∵S
n<3,
∴4-
<3
∴n+2>2
n-1,
分别画出函数y=x+2(x>0),与y=2
x-1(x>0)的图象,如图所示
由图象可知,当n=1,2,3时,S
n<3成立.
点评:本题考查二次函数的性质,以及等差关系的确定,错位相减法求数列的和,培养可学生的转化思想与综合运算、推理证明能力,属于中档题.

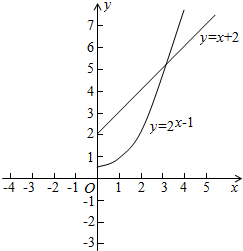 证明:(1)∵二次函数f(x)=
证明:(1)∵二次函数f(x)=

 名校课堂系列答案
名校课堂系列答案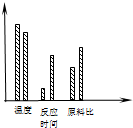 如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )
如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )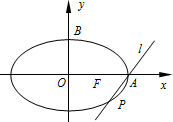 在平面直角坐标系xOy中,椭圆C:
在平面直角坐标系xOy中,椭圆C: