
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且b=acosc+ ![]() csinA.
csinA.
(1)求角A的大小;
(2)当a=3时,求△ABC周长的取值范围.
【答案】
(1)解:由 ![]() 及正弦定理得,
及正弦定理得, ![]() ,
,
∵B=π﹣(A+C),
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵C∈(0,π),
∴sinC≠0,
∴ ![]()
易知cosA≠0,
∴ ![]() ,
,
∵A∈(0,π)
∴ ![]() .
.
(2)解:由余弦定理a2=b2+c2﹣2bccosA,得9=b2+c2﹣bc
∵b2+c2≥2bc,当且仅当b=c时,“=”成立,…(8分)
∴9=b2+c2﹣bc≥bc,即bc≤9,当且仅当b=c=3时,“=”成立,
又由9=b2+c2﹣bc=(b+c)2﹣3bc,得(b+c)2=9+3bc≤36,
∴b+c≤6,
∵b+c>3,
∴6<a+b+c≤9
∴求△ABC周长的取值范围(6,9].
【解析】(1)由已知及正弦定理,三角形内角和定理,三角函数恒等变换的应用,可得 ![]() ,
,
又sinC≠0,可求 ![]() ,结合范围A∈(0,π),即可求得A的值.(2)由余弦定理得9=b2+c2﹣bc,利用基本不等式可求bc≤9,又由9=b2+c2﹣bc=(b+c)2﹣3bc,得b+c≤6,又b+c>3,可得范围6<a+b+c≤9.
,结合范围A∈(0,π),即可求得A的值.(2)由余弦定理得9=b2+c2﹣bc,利用基本不等式可求bc≤9,又由9=b2+c2﹣bc=(b+c)2﹣3bc,得b+c≤6,又b+c>3,可得范围6<a+b+c≤9.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 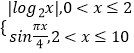 .
.
(1)设函数g(x)=f(x)﹣1,求函数g(x)的零点;
(2)若函数f(x1)=f(x2)=f(x3)=f(x4),且0<x1<x2<x3<x4≤10,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四点F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求证:平面CBE⊥平面EDB;
(Ⅲ)当x=2时,求二面角F﹣EB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  ,设F(x)=x2f(x),则F(x)是( )
,设F(x)=x2f(x),则F(x)是( )
A.奇函数,在(﹣∞,+∞)上单调递减
B.奇函数,在(﹣∞,+∞)上单调递增
C.偶函数,在(﹣∞,0)上递减,在(0,+∞)上递增
D.偶函数,在(﹣∞,0)上递增,在(0,+∞)上递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )满足
)满足 ![]() =2,且
=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,则
|=3,则 ![]()
![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com