
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() .
.
(ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(ⅱ)求函数![]() 在区间
在区间![]() 内的极大值的个数.
内的极大值的个数.
(2)若![]() 在
在![]() 内单调递减,求实数
内单调递减,求实数![]() 的取值范围.
的取值范围.
【答案】(1)(ⅰ)![]() ;(ⅱ)1;(2)
;(ⅱ)1;(2)![]() .
.
【解析】
(1)(ⅰ)求出导函数,得到![]() 与
与![]() ,利用点斜式得到直线的方程;(ⅱ)研究函数在区间
,利用点斜式得到直线的方程;(ⅱ)研究函数在区间![]() 内单调性,结合极值的定义得到答案;
内单调性,结合极值的定义得到答案;
(2)由题可知![]() ,其中
,其中![]() ,分两类情况:
,分两类情况:![]() 与
与![]() ,
,
结合函数的单调性与极值即可得到实数![]() 的取值范围.
的取值范围.
(1)(ⅰ)因为![]() ,
,
所以![]() ,
,![]() .
.
又因为![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
化简得![]() .
.
(ⅱ)当![]() 时,
时,![]() ,
,![]() 单调递增,此时
单调递增,此时![]() 无极大值.
无极大值.
当![]() 时,设
时,设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 内单调递减.
内单调递减.
又因为![]() ,
, ![]() ,
,
所以在![]() 内存在唯一的
内存在唯一的![]() ,使得
,使得![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化如下表
的变化如下表
|
|
|
|
|
| 0 |
|
| ↗ | ↘ |
所以![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,此时
内单调递减,此时![]() 有唯一极大值.
有唯一极大值.
综上所述,![]() 在
在![]() 内的极大值的个数为
内的极大值的个数为![]() .
.
(2) 由题可知![]() ,其中
,其中![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减;
内单调递减;
下面设![]() .
.
对于![]() ,
,![]() ,且
,且![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() .
.
设![]() ,
,![]() ,
,
则![]() .
.
所以![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,
, ![]() .
.
当![]() 时,即
时,即![]() 时,
时,![]() ,对
,对![]() ,
,![]() ,
,
所以![]() ,
,![]() 在
在![]() 内单调递增,不符合题意.
内单调递增,不符合题意.
当![]() 时,即
时,即![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,使
,使![]() ,
,
因为![]() 在
在![]() 内单调递减,
内单调递减,
所以对![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 内单调递增,不符合题意.
内单调递增,不符合题意.
所以当![]() 时,
时,![]() 在
在![]() 内不单调递减.
内不单调递减.
综上可得![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点P的轨迹![]() ;
;
(2)直线![]() 与曲线
与曲线![]() 交于不同的两点A,B(A,B在
交于不同的两点A,B(A,B在![]() 轴的上方)
轴的上方)![]() :
:
①当A为椭圆与![]() 轴的正半轴的交点时,求直线
轴的正半轴的交点时,求直线![]() 的方程;
的方程;
②对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相切,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类是改善环境,节约资源的新举措.住建部于6月28日拟定了包括我市在内的46个重点试点城市,要求这些城市在2020年底基本建成垃圾分类处理系统.为此,我市某中学对学生开展了“垃圾分类”有关知识的讲座并进行测试,将所得测试成绩整理后,绘制出频率分布直方图如图所示.

(1)求频率分布直方图中a的值,并估计测试的平均成绩;
(2)将频率视为相应的概率,如果从参加测试的同学中随机选取4名同学,这4名同学中测试成绩在![]() 的人数记为
的人数记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛、马和羊,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,则让三位同学选取的礼物都满意的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位?
某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
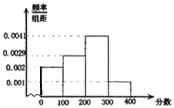
试结合此频率分布直方图估计:
(1)此次考试的中位数是多少分(保留为整数)?
(2)若考生甲的成绩为280分,能否被录取?若能被录取,能否获得高薪职位?(分数精确到个位,概率精确到千分位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 折起到
折起到![]() (
(![]() 平面
平面![]() )的位置,
)的位置,![]() 为线段
为线段![]() 的中点.
的中点.
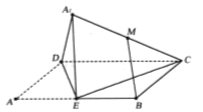
(1)求证:![]() 平面
平面![]() ;
;
(2)已知![]() ,当平面
,当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com