
【题目】已知动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点P的轨迹![]() ;
;
(2)直线![]() 与曲线
与曲线![]() 交于不同的两点A,B(A,B在
交于不同的两点A,B(A,B在![]() 轴的上方)
轴的上方)![]() :
:
①当A为椭圆与![]() 轴的正半轴的交点时,求直线
轴的正半轴的交点时,求直线![]() 的方程;
的方程;
②对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
【答案】(1)动点P的轨迹![]() 为:
为:![]() ,是中心在原点、焦点在
,是中心在原点、焦点在![]() 轴、长轴长为2
轴、长轴长为2![]() 、短轴长为2的椭圆;(2) ①
、短轴长为2的椭圆;(2) ①![]() ,②存在定点
,②存在定点![]() ,满足题意,证明见解析.
,满足题意,证明见解析.
【解析】
(1)利用点到直线的距离公式和两点之间距离公式,化简整理即可得出动点P的轨迹;
(2) ①求直线FB:![]() 和椭圆联立求B点坐标,然后利用两点式求直线
和椭圆联立求B点坐标,然后利用两点式求直线![]() 方程;
方程;
②设直线![]() 方程
方程![]() 和椭圆联立消元化简,由
和椭圆联立消元化简,由![]() 得
得![]() ,然后利用韦达定理代入化简可得
,然后利用韦达定理代入化简可得![]() ,代入直线方程
,代入直线方程![]() 即可求得答案.
即可求得答案.
(1)设点P(![]() ),则P点到直线
),则P点到直线![]() 的距离
的距离![]() ,P点到点
,P点到点![]() 的距离
的距离![]() ,由题意
,由题意![]() ,得
,得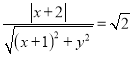 ,化简整理得:
,化简整理得:![]()
所以动点P的轨迹![]() 为:
为:![]() ,是中心在原点、焦点在
,是中心在原点、焦点在![]() 轴、长轴长为2
轴、长轴长为2![]() 、短轴长为2的椭圆.
、短轴长为2的椭圆.
(2)由题意直线![]() 与曲线
与曲线![]() 交于不同的两点A,B(A,B在
交于不同的两点A,B(A,B在![]() 轴的上方),可得直线
轴的上方),可得直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,由
,由![]() ,可得
,可得![]() .
.
①由(1)得曲线![]()
![]() ,则得A(0,1),F(-1,0),所以
,则得A(0,1),F(-1,0),所以![]() ,
,![]() ,所以直线FB的方程为
,所以直线FB的方程为![]() ,由
,由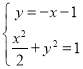 联立消
联立消![]() 得
得![]() 解得
解得![]() 或
或![]() ,
,
代入![]() ,可得交点坐标:(0,-1),(
,可得交点坐标:(0,-1),(![]() ),由B点在
),由B点在![]() 轴上方则可得B点坐标为(
轴上方则可得B点坐标为(![]() ),则由两点式可得直线
),则由两点式可得直线![]() :
: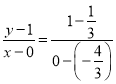 ,化简得
,化简得![]() .
.
②存在定点![]() ,满足题意,证明如下:
,满足题意,证明如下:
设A(![]() ),B(
),B(![]() )
)
由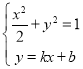 消
消![]() 化简得
化简得![]()
则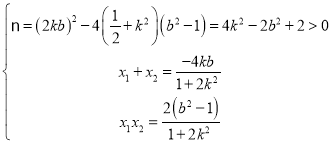 ,
,
所以由![]() ,
,![]() ,
,![]() 可得
可得![]()
化简得![]() ,代入
,代入![]() 和
和![]()
化简得![]() ,所以直线
,所以直线![]() 方程为:
方程为:![]() ,可得直线恒过点
,可得直线恒过点![]() ,
,
故无论![]() 如何变化,满足题意的直线
如何变化,满足题意的直线![]() 恒过定点
恒过定点![]() .
.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若过![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且sin2A+sin2B+sin2C=sinAsinB+sinBsinC+sinCsin A.
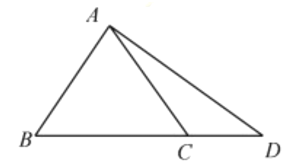
(1)证明:△ABC是正三角形;
(2)如图,点D在边BC的延长线上,且BC=2CD,AD![]() ,求sin∠BAD的值.
,求sin∠BAD的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士数学家、物理学家欧拉发现任一凸多面体(即多面体内任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数V、棱数E及面数F满足等式V﹣E+F=2,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮、简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,它是由12块黑色正五边形面料和20块白色正六边形面料构成的.20世纪80年代,化学家们成功地以碳原子为顶点组成了该种结构,排列出全世界最小的一颗“足球”,称为“巴克球(Buckyball)”.则“巴克球”的顶点个数为( )

A.180B.120C.60D.30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com