练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】瑞士数学家、物理学家欧拉发现任一凸多面体（即多面体内任意两点的连线都被完全包含在该多面体中，直观上讲是指没有凹陷或孔洞的多面体）的顶点数V、棱数E及面数F满足等式V﹣E+F＝2，这个等式称为欧拉多面体公式，被认为是数学领域最漂亮、简洁的公式之一，现实生活中存在很多奇妙的几何体，现代足球的外观即取自一种不完全正多面体，它是由12块黑色正五边形面料和20块白色正六边形面料构成的．20世纪80年代，化学家们成功地以碳原子为顶点组成了该种结构，排列出全世界最小的一颗“足球”，称为“巴克球（Buckyball）”．则“巴克球”的顶点个数为（ ）

    A.180B.120C.60D.30

    【答案】C

    【解析】

    设巴克球顶点数、棱数及面数，计算出面数和棱数即可求出顶点数．

    解：依题意，设巴克球顶点数、棱数及面数，

    则，

    每条棱被两个面公用，故棱数，

    所以由得：，解得．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表：

    年份

    2014

    2015

    2016

    2017

    2018

    销量（万台）

    8

    10

    13

    25

    24

    某机构调查了该地区30位购车车主的性别与购车种类情况，得到的部分数据如下表所示：

    购置传统燃油车

    购置新能源车

    总计

    男性车主

    6

    24

    女性车主

    2

    总计

    30

    （1）求新能源乘用车的销量关于年份的线性相关系数，并判断与是否线性相关；

    （2）请将上述列联表补充完整，并判断是否有的把握认为购车车主是否购置新能源乘用车与性别有关；

    （3）若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.

    参考公式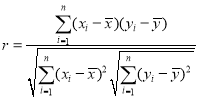：，，其中.，若，则可判断与线性相关.

    附表：

    0．10

    0.05

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）对任意的，，，恒有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动点P到直线的距离与到点的距离之比为.

    （1）求动点P的轨迹；

    （2）直线与曲线交于不同的两点A,B(A,B在轴的上方)：

    ①当A为椭圆与轴的正半轴的交点时，求直线的方程；

    ②对于动直线，是否存在一个定点，无论如何变化，直线总经过此定点？若存在，求出该定点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为，（t为参数），在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C1：ρ＝2cosθ，．

    （1）求C1与C2交点的直角坐标；

    （2）若直线l与曲线C1，C2分别相交于异于原点的点M，N，求|MN|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为，（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为（ρ﹣2cosθ）2＝5﹣4sin2θ．

    （1）求直线l的普通方程和曲线C的直角坐标方程；

    （2）若直线l与曲线C相切，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】垃圾分类是改善环境，节约资源的新举措．住建部于6月28日拟定了包括我市在内的46个重点试点城市，要求这些城市在2020年底基本建成垃圾分类处理系统．为此，我市某中学对学生开展了“垃圾分类”有关知识的讲座并进行测试，将所得测试成绩整理后，绘制出频率分布直方图如图所示．

    （1）求频率分布直方图中a的值，并估计测试的平均成绩；

    （2）将频率视为相应的概率，如果从参加测试的同学中随机选取4名同学，这4名同学中测试成绩在的人数记为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“公平正义”是社会主义和谐社会的重要特征，是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径，正被广泛采用.每次考试过后，考生最关心的问题是:自己的考试名次是多少？自已能否被录取?能获得什么样的职位？

    某单位准备通过考试(按照高分优先录取的原则)录用名，其中个高薪职位和个普薪职位.实际报名人数为名，考试满分为分. 考试后对部分考生考试成绩进行抽样分析，得到频率分布直方图如下：

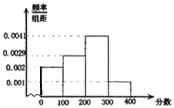
    试结合此频率分布直方图估计：

    (1)此次考试的中位数是多少分（保留为整数）？

    (2)若考生甲的成绩为280分，能否被录取?若能被录取，能否获得高薪职位？(分数精确到个位，概率精确到千分位)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果对一切正实数，，不等式恒成立，则实数的取值范围是（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案