Question

【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且sin2A+sin2B+sin2C＝sinAsinB+sinBsinC+sinCsin A．

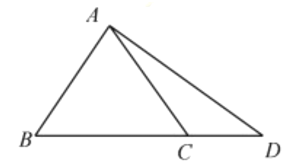
（1）证明：△ABC是正三角形；

（2）如图，点D在边BC的延长线上，且BC＝2CD，AD，求sin∠BAD的值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）由已知利用正弦定理可得，再配方得，则，因此是正三角形；

（2）由已知条件可得，，再由余弦定理可得，又，利用正弦定理即可得到结论.

（1）证明：∵sin2A+sin2B+sin2C＝sinAsinB+sinBsinC+sinCsin A

∴a2+b2+c2＝ab+ac+bc，∴2a2+2b2+2c2＝2ab+2ac+2bc，

∴（a﹣b）2+（b﹣c）2+（a﹣c）2＝0，∴a＝b＝c，

∴△ABC为等边三角形；

（2）∵△ABC是等边三角形，BC＝2CD，

∴AC＝2CD，∠ACD＝120°，

∴在△ACD中，由余弦定理，得AD2＝AC2+CD2﹣2ACCDcos∠ACD，

∴7＝4CD2+CD2﹣4CDCDcos120°，∴CD＝1，

在△ABC中，BD＝3CD＝3，

由正弦定理，得sin∠BAD．