
【题目】已知点Pn(an,bn)满足an+1=an·bn+1,bn+1=![]() (n∈N*),且点P1的坐标为(1,-1).
(n∈N*),且点P1的坐标为(1,-1).
(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上
【答案】(1)2x+y=1(2)证明见解析
【解析】
(1)求出P2的坐标,列出直线的两点式方程,化简即可;
(2)由(1)知,n=1时,2a1+b1=1成立,假设n=k时,2ak+bk=1成立,进而证得当n=k+1时,2ak+1+bk+1=1也成立,故n∈N*,Pn都在直线l上.
(1)由题意得a1=1,b1=-1,故b2=![]() ,a2=1×
,a2=1×![]() =
=![]() ,∴P2
,∴P2![]() .
.
∴直线l的方程为 ,即2x+y=1.
,即2x+y=1.
(2)证明:①当n=1时,由(1)知,2a1+b1=2×1+(-1)=1成立,
②假设n=k(k≥1且k∈N*)时,2ak+bk=1成立.
当n=k+1时,则![]()
∴当n=k+1时,2ak+1+bk+1=1也成立.
由①②知,对于n∈N*,都有2an+bn=1,
即点Pn在直线l上.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率是
)的离心率是![]() ,
,![]() ,
,![]() 分别为椭圆E的左右顶点,B为上顶点,
分别为椭圆E的左右顶点,B为上顶点,![]() 的面积为2.直线l过点
的面积为2.直线l过点![]() 且与椭圆E交于P,Q两点(P,Q异于
且与椭圆E交于P,Q两点(P,Q异于![]() ,
,![]() )
)
(1)求椭圆E的标准方程;
(2)求![]() 的面积最大值;
的面积最大值;
(3)设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为常数,并求出这个常数.
为常数,并求出这个常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且sin2A+sin2B+sin2C=sinAsinB+sinBsinC+sinCsin A.
(1)证明:△ABC是正三角形;
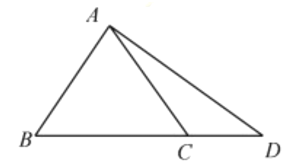
(2)如图,点D在边BC的延长线上,且BC=2CD,AD![]() ,求sin∠BAD的值.
,求sin∠BAD的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三课外兴趣小组为了了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
附:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线交双曲线的右支于点
的切线交双曲线的右支于点![]() ,且切点为
,且切点为![]() ,已知
,已知![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点(
的中点(![]() 点在切点
点在切点![]() 的右侧),若
的右侧),若![]() 的周长为
的周长为![]() ,则双曲线的渐近线的方程为( )
,则双曲线的渐近线的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com