
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其短半轴长为
,其短半轴长为![]() ,一个焦点坐标为
,一个焦点坐标为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上的点,且
上的点,且![]() .
.
![]() 证明:直线
证明:直线![]() 与圆
与圆![]() 相切;
相切;
![]() 求
求![]() 面积的最小值.
面积的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
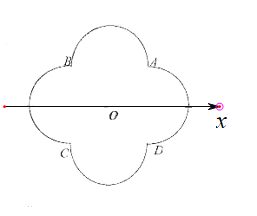
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (
(![]() ,
,![]() )的一条渐近线方程为
)的一条渐近线方程为![]() ,点
,点![]() 在双曲线上;抛物线
在双曲线上;抛物线![]() (
(![]() )的焦点F与双曲线的右焦点重合.
)的焦点F与双曲线的右焦点重合.
(1)求双曲线和抛物线的标准方程;
(2)过焦点F作一条直线l交抛物线于A,B两点,当直线l的斜率为![]() 时,求线段
时,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Pn(an,bn)满足an+1=an·bn+1,bn+1=![]() (n∈N*),且点P1的坐标为(1,-1).
(n∈N*),且点P1的坐标为(1,-1).
(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了该种药用昆虫的6组观测数据如下表:
温度x/℃ | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得:
![]() ,
,![]() ,
,![]() 线性回归模型的残差平方和
线性回归模型的残差平方和![]() ,
,![]() ,
,
其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求y关于x的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求得y关于x的回归方程为![]() ,且相关指数
,且相关指数![]() .
.
①试与1中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为35℃时该用哪种药用昆虫的产卵数(结果取整数)
附:一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系中,以原点为极点,以![]() 轴非负半轴为极轴建立极坐标系, 已知曲线
轴非负半轴为极轴建立极坐标系, 已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() (
(![]() 是常数,且
是常数,且![]() ).
).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() ,
,![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为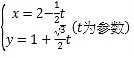 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com