
【题目】己知函数![]() (
(![]() 是常数,且
是常数,且![]() ).
).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() ,
,![]() 时,
时,![]() .
.
【答案】(1)单调递减区间为![]() ,单调递增区间是
,单调递增区间是![]() ;
;
(2)实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)证明见详解;
【解析】
(1)先求导,再根据导数与函数的单调性的关系即可得到.
(2)![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() ,解得
,解得![]() ,关于
,关于![]() 的方程
的方程![]() 化为
化为![]() ,令
,令![]() (
(![]() ),利用导数研究单调性极值与最值,关于
),利用导数研究单调性极值与最值,关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,必须满足
上恰有两个不相等的实数根,必须满足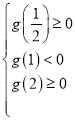 解得即可.
解得即可.
(3)由(1)和(2)可知当![]() 时,
时,![]() ,即
,即![]() ,可得当
,可得当![]() 时,
时,![]() ,令
,令![]() ,则
,则![]() ,利用“累加法求和”、对数的运算性质、放缩、“裂项求和”即可证出.
,利用“累加法求和”、对数的运算性质、放缩、“裂项求和”即可证出.
(1)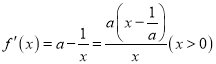
若![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,
,
![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)![]()
![]() 在
在![]() 处取得极值,
处取得极值,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,
关于![]() 的方程
的方程![]() 化为
化为![]() ,
,
令![]() (
(![]() ),
),
![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 单调递增,
单调递增,
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 单调递减,
单调递减,
![]() 关于
关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
则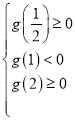 ,即
,即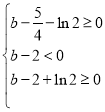 ,解得
,解得![]() ,
,
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() .
.
(3)由(1)和(2)可知,当![]() 时,
时,![]() ,即
,即![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() ,
,
依次取![]() ,
,
累加求和可得
![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() ,
,![]() 时,
时,
![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线交双曲线的右支于点
的切线交双曲线的右支于点![]() ,且切点为
,且切点为![]() ,已知
,已知![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点(
的中点(![]() 点在切点
点在切点![]() 的右侧),若
的右侧),若![]() 的周长为
的周长为![]() ,则双曲线的渐近线的方程为( )
,则双曲线的渐近线的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() ,
,![]() ,
,![]() ,给出下列命题,其中真命题是( )
,给出下列命题,其中真命题是( )
A.“![]() ”是“
”是“![]() ”的充要条件B.“
”的充要条件B.“![]() ”是“
”是“![]() ”的充分条件
”的充分条件
C.“![]() ”是“
”是“![]() ”的必要条件D.“
”的必要条件D.“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件
是无理数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列![]() 前
前![]() 项和为
项和为![]() ,且满足
,且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 前
前![]() 项和
项和![]() ;
;
(3)在数列![]() 中,是否存在连续的三项
中,是否存在连续的三项![]() ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
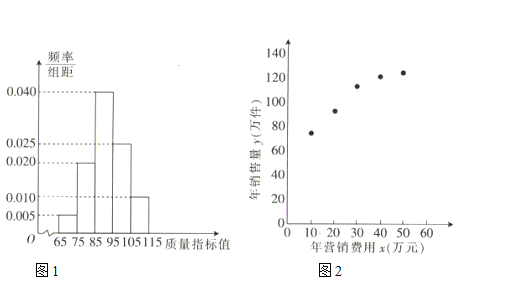
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为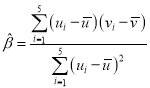 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com