
分析 (1)利用已知条件之间求解z2,z3,z4.
(2)求出${z_n}={(1+i)^{n-1}}{z_1}$,利用复数的幂运算,求解即可.
(3)通过${z_{n+4}}={(1+i)^4}{z_n}=-4{z_n}$,推出xn+4=-4xn,yn+4=-4yn,得到xn+4yn+4=16xnyn,然后求解数列的和即可.
解答 本题(18分),第1小题(4分),第2小题(6分),第3小题(8分).
解:(1)z2=(1+i)(3+4i)=-1+7i,z3=-8+6i,z4=-14-2i.…(4分)
(算错一个扣(1分),即算对一个得(2分),算对两个得3分)
(2)若$\overrightarrow{O{Z_n}}$∥$\overrightarrow{O{Z_1}}$,则存在实数λ,使得$\overrightarrow{O{Z_n}}=λ\overrightarrow{O{Z_1}}$,故zn=λ•z1,
即(xn,yn)=λ(x1,y1),…(3分)
又zn+1=(1+i)zn,故${z_n}={(1+i)^{n-1}}{z_1}$,即(1+i)n-1=λ为实数,…(5分)
故n-1为4的倍数,即n-1=4k,n=4k+1,k∈N. …(6分)
(3)因为${z_{n+4}}={(1+i)^4}{z_n}=-4{z_n}$,故xn+4=-4xn,yn+4=-4yn,…(2分)
所以xn+4yn+4=16xnyn,…(3分)
又x1y1=12,x2y2=-7,x3y3=-48,x4y4=28,
x1y1+x2y2+x3y3+…+x100y100
=(x1y1+x2y2+x3y3+x4y4)+(x5y5+x6y6+x7y7+x8y8)+…+(x97y97+x98y98+x99y99+x100y100)
=$(12-7-48+28)•\frac{{1-{{16}^{25}}}}{1-16}=1-{2^{100}}$,…(6分)
而${x_{101}}{y_{101}}={16^{25}}{x_1}{y_1}=12×{2^{100}}$,${x_{102}}{y_{102}}={16^{25}}{x_2}{y_2}=-7×{2^{100}}$,…(7分)
所以数列{xnyn}的前102项之和为1-2100+12×2100-7×2100=1+2102.…(8分)
点评 本题考查复数的基本运算,复数的代数形式混合运算,考查数列求和,考查计算能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 123.56 | 21.45 | -7.82 | 11.45 | -53.76 | -128.88 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
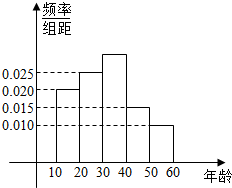 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com