
| A. | π | B. | $\frac{3}{2}π$ | C. | 3π | D. | $\frac{5}{2}π$ |
分析 本题首先要弄清楚曲线的形状,再根据曲线的性质及解析几何知识即可求出长度.
解答  解:此问题的实质是以A为球心,以2为半径的在正方体ABCD-A1B1C1D1各个面上交线的长度计算,正方体的各个面根据与球心位置关系分成两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,各弧圆心角为$\frac{π}{6}$,A1B1C1D1、B1BCC1、D1DCC1为与球心距离为1的截面,截痕为小圆弧,由于截面圆半径为
解:此问题的实质是以A为球心,以2为半径的在正方体ABCD-A1B1C1D1各个面上交线的长度计算,正方体的各个面根据与球心位置关系分成两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,各弧圆心角为$\frac{π}{6}$,A1B1C1D1、B1BCC1、D1DCC1为与球心距离为1的截面,截痕为小圆弧,由于截面圆半径为
r=1,故各段弧圆心角为 $\frac{π}{2}$,∴这条曲线长度为$l=3×\frac{π}{6}×2+3×\frac{π}{2}×1=\frac{5π}{2}$,
∴故答案为:D.
点评 本题考查弧长公式的应用,解题时要认真审题,仔细观察,避免出错,弧长公式;棱柱的结构特征.


科目:高中数学 来源: 题型:选择题
| A. | P>Q>M | B. | Q>P>M | C. | Q>M>P | D. | M>Q>P |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{3π}{8}$,2kπ+$\frac{π}{8}$](k∈Z) | B. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5π}{8}$](k∈Z) | ||
| C. | [kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$](k∈Z) | D. | [kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | [0,4) | C. | (0,5] | D. | [0,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 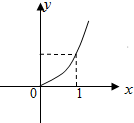 | ||
| C. | 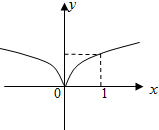 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 6 | C. | $\sqrt{14}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com