
.(本小题满分12分)
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,f(x)>0,
当x∈(-∞,-2)∪(6 ,+∞)时,f(x)<0,
,+∞)时,f(x)<0,
(1)求f(x)的解析式.
(2)求f(x)在区间[1,10]上的最值。
科目:高中数学 来源: 题型:解答题
某工厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价恰为51元;
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少?如果订购1 000个,利润又是多少?(工厂售出一个零件的利润=实际出厂单价-成本
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
((本题满分15分)
已知三个函数 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的 为同一个常数,且
为同一个常数,且 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程 的三个根.
的三个根.
(Ⅰ) 求证: ;
;
(Ⅱ) 设 是函数
是函数 的两个极值点,求
的两个极值点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
函数 (
( 为常数)的图象过点
为常数)的图象过点 ,
,
(Ⅰ)求 的值并判断
的值并判断 的奇偶性;
的奇偶性;
(Ⅱ)函数 在区间
在区间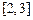 上
上 有意义,求实数
有意义,求实数 的取值范围;
的取值范围;
(Ⅲ)讨论关于 的方程
的方程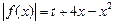
 (
( 为常数)的正根的个数.
为常数)的正根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第
为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第 小时教室内每立方米空气中的含药量为
小时教室内每立方米空气中的含药量为 毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为 (a为常数).函数图象如图所示.
(a为常数).函数图象如图所示.
根据图中提供的信息,解答下列问题:
(1)求从药物释放开始每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
|

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作 横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数 在其定义域上满足
在其定义域上满足 .
.
(1)函数 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当 时,求x的取值范围;
时,求x的取值范围;
(3)若 ,数列
,数列 满足
满足 ,那么:
,那么:
①若 ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
,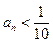 恒成立,求最小的N;
恒成立,求最小的N;
②若 ,求证:
,求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com