
【题目】已知四面体有五条棱长为3,且外接球半径为2.动点P在四面体的内部或表面,P到四个面的距离之和记为s.已知动点P在![]() ,
,![]() 两处时,s分别取得最小值和最大值,则线段
两处时,s分别取得最小值和最大值,则线段![]() 长度的最小值为______.
长度的最小值为______.
【答案】![]()
【解析】
设四面体为![]() ,其中
,其中![]() ,取
,取![]() 的中点分别为
的中点分别为![]() ,求出
,求出![]() 的长,将点
的长,将点![]() 到四个面的距离之和记为s,转化为到其中两个面的距离,利用等体积的方法分析出距离之和的最值,从而得到线段
到四个面的距离之和记为s,转化为到其中两个面的距离,利用等体积的方法分析出距离之和的最值,从而得到线段![]() 长度的最小值为
长度的最小值为![]() ,
,![]() 上两点间的距离的最小值,得到答案.
上两点间的距离的最小值,得到答案.
四面体为![]() ,其中
,其中![]() ,设
,设![]() .
.
取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,如图.
,如图.
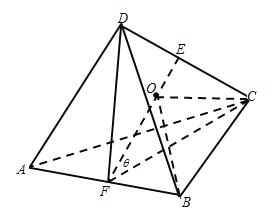
在等腰三角形![]() 中,有
中,有![]() .
.
所以![]() 平面
平面![]() ,又
,又![]() 为
为![]() 的中点.
的中点.
则四面体![]() 的外接球的球心
的外接球的球心![]() 一定在平面
一定在平面![]() 上.
上.
同理可得四面体![]() 的外接球的球心
的外接球的球心![]() 一定在平面
一定在平面![]() 上.
上.
所以四面体![]() 的外接球的球心
的外接球的球心![]() 一定在
一定在![]() 上.
上.
连接![]() ,设
,设![]() .
.
在直角三角形![]() 中,
中,![]() .
.
在三角形![]() 中,
中,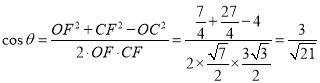 .
.
在直角三角形![]() 中,
中,![]() .
.
所以![]() 长为定值,
长为定值,![]() 的长为定值.
的长为定值.
根据条件有![]() ,设为
,设为![]() ,
, ![]() ,设为
,设为![]()
设点![]() 到四个面
到四个面![]() ,
,![]() ,
,![]() ,
,![]() 的距离分别为
的距离分别为![]() .
.
设四面体![]() 的体积为
的体积为![]() (为定值)
(为定值)
由等体积法有:![]()
所以![]()
所以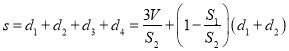
当点![]() 在
在![]() 上时,
上时,![]() 最小.
最小.
当点![]() 远离
远离![]() 时,
时,![]() 的值增大,
的值增大,
由等体积法可得当点![]() 在
在![]() 上时,
上时,![]() 的值相等,且此时
的值相等,且此时![]() 的值最大.
的值最大.
所以当点![]() 在
在![]() 或
或![]() 上时,
上时,![]() 取得最值.
取得最值.
故线段![]() 长度的最小值为
长度的最小值为![]() ,
,![]() 上两点间的距离的最小值.
上两点间的距离的最小值.
由上可知,![]() .
.
所以![]() ,
,![]() 上两点间的距离的最小值为
上两点间的距离的最小值为![]() .
.
故答案为:![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某地实行垃圾分类后,政府决定为![]() 三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知
三个小区建造一座垃圾处理站M,集中处理三个小区的湿垃圾.已知![]() 在
在![]() 的正西方向,
的正西方向,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,
方向,![]() 在
在![]() 的北偏西
的北偏西![]() 方向,且在
方向,且在![]() 的北偏西
的北偏西![]() 方向,小区
方向,小区![]() 与
与![]() 相距
相距![]() 与
与![]() 相距
相距![]() .
.
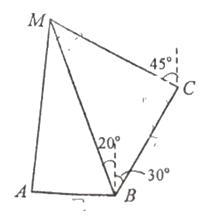
(1)求垃圾处理站![]() 与小区
与小区![]() 之间的距离;
之间的距离;
(2)假设有大、小两种运输车,车在往返各小区、处理站之间都是直线行驶,一辆大车的行车费用为每公里![]() 元,一辆小车的行车费用为每公里
元,一辆小车的行车费用为每公里![]() 元(其中
元(其中![]() 为满足
为满足![]() 是
是![]() 内的正整数) .现有两种运输湿垃圾的方案:
内的正整数) .现有两种运输湿垃圾的方案:
方案1:只用一辆大车运输,从![]() 出发,依次经
出发,依次经![]() 再由
再由![]() 返回到
返回到![]() ;
;
方案2:先用两辆小车分别从![]() 运送到
运送到![]() ,然后并各自返回到
,然后并各自返回到![]() ,一辆大车从
,一辆大车从![]() 直接到
直接到![]() 再返回到
再返回到![]() .试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
.试比较哪种方案更合算?请说明理由. 结果精确到小数点后两位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )

A.33B.56C.64D.78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何是美籍法国数学家芒德勃罗在20世纪70年代创立的一门数学新分支,其中的“谢尔宾斯基”图形的作法是:先作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的每个小正三角形中又挖去一个“中心三角形”.按上述方法无限连续地作下去直到无穷,最终所得的极限图形称为“谢尔宾斯基”图形(如图所示),按上述操作7次后,“谢尔宾斯基”图形中的小正三角形的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com