
【题目】已知sinα+cosα= ![]() ,α∈(0,
,α∈(0, ![]() ),sin(β﹣
),sin(β﹣ ![]() )=
)= ![]() ,β∈(
,β∈( ![]() ,
, ![]() ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值.
【答案】
(1)解:由题意得(sinα+cosα)2= ![]() ,
,
即1+sin2α= ![]() ,∴sin2α=
,∴sin2α= ![]() .
.
又2α∈(0, ![]() ),∴cos2α=
),∴cos2α= ![]() =
= ![]() ,∴tan2α=
,∴tan2α= ![]() =
= ![]()
(2)解:∵β∈( ![]() ,
, ![]() ),β﹣
),β﹣ ![]() ∈(0,
∈(0, ![]() ),∴cos(β﹣
),∴cos(β﹣ ![]() )=
)= ![]() ,
,
于是sin2(β﹣ ![]() )=2sin(β﹣
)=2sin(β﹣ ![]() )cos(β﹣
)cos(β﹣ ![]() )=
)= ![]() .
.
又sin2(β﹣ ![]() )=﹣cos2β,∴cos2β=﹣
)=﹣cos2β,∴cos2β=﹣ ![]() .
.
又2β∈( ![]() ,π),∴sin2β=
,π),∴sin2β= ![]() .
.
又cos2α= ![]() =
= ![]() ,
,
∴cosα= ![]() ,sinα=
,sinα= ![]() (α∈(0,
(α∈(0, ![]() )).
)).
∴cos(α+2β)=cosαcos2β﹣sinαsin2β
= ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() =﹣
=﹣ ![]()
【解析】(1)把已知条件两边平方,然后利用同角三角函数间的关系及二倍角的正弦函数公式化简可得sin2α的值,根据2α的范围利用同角三角函数间的关系求出cos2α即可得到tan2α的值;(2)根据β的范围求出 ![]() 的范围,由sin(
的范围,由sin( ![]() )的值利用同角三角函数间的关系求出cos(
)的值利用同角三角函数间的关系求出cos( ![]() )的值,然后利用二倍角的正弦函数公式及同角三角函数间的关系分别求出sin2β和cos2β的值,根据第一问分别求出sinα和cosα的值,把所求的式子利用两角和的余弦函数公式化简后,将每个三角函数值代入即可求出.
)的值,然后利用二倍角的正弦函数公式及同角三角函数间的关系分别求出sin2β和cos2β的值,根据第一问分别求出sinα和cosα的值,把所求的式子利用两角和的余弦函数公式化简后,将每个三角函数值代入即可求出.
【考点精析】本题主要考查了两角和与差的余弦公式和二倍角的正弦公式的相关知识点,需要掌握两角和与差的余弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
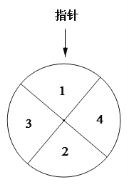
【题目】【2016高考山东文数】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个; ③其余情况奖励饮料一瓶.
,则奖励水杯一个; ③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).
).
(Ⅰ)把曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(Ⅱ)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
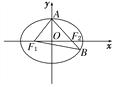
【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
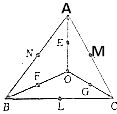
【题目】平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)试用 ![]() ,
, ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() ,
, ![]() ;
;
(2)证明:线段EL,FM,GN交于一点且互相平分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com