
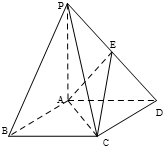
 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PA=AB=2,BC=$\frac{1}{2}$PA,BD=$\sqrt{3}$,E在PC边上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PA=AB=2,BC=$\frac{1}{2}$PA,BD=$\sqrt{3}$,E在PC边上.分析 (1)由题意可得AD2+BD2=AB2,得AD⊥BD,再由PD⊥底面ABCD,得BD⊥平面PAD,由面面垂直的判定得平面PDA⊥平面PDB;
(2)以D为原点建立如图3所示空间直角坐标系,由已知得到点D、P、A、B、C、E的坐标,由$\overrightarrow{AP}、\overrightarrow{BE}$的夹角求得异面直线AP与BE所成角的余弦值;
(3)由C,E,P三点共线,得$\overrightarrow{DE}=λ\overrightarrow{DP}+(1-λ)\overrightarrow{DC}$,且0≤λ≤1,从而求出$\overrightarrow{DE}、\overrightarrow{DB}$的坐标,再求出平面EDB与平面CBD的法向量,结合二面角E-BD-C的大小为30°列式求得λ,进一步得到$\overrightarrow{DE}$的坐标,则DE的长可求.
解答 (1)证明:∵底面ABCD是平行四边形,∴AD=BC=1,
又$BD=\sqrt{3},\;\;AB=2$,满足AD2+BD2=AB2,
∴AD⊥BD,
又∵PD⊥底面ABCD,∴PD⊥BD,得BD⊥平面PAD,
∵BD?平面PDB,∴平面PDA⊥平面PDB;
(2)解:以D为原点建立如图3所示空间直角坐标系,
则$D(0,\;\;0,\;\;0),\;\;P(0,\;\;0,\;\;\sqrt{3}),\;\;A(1,\;\;0,\;\;0),\;\;B(0,\;\;\sqrt{3},\;\;0)$,$C(-1,\;\;\sqrt{3},\;\;0)$,
∵E是PC边上的中点,∴$E({-\frac{1}{2},\;\;\frac{{\sqrt{3}}}{2},\;\;\frac{{\sqrt{3}}}{2}\;})$,
则$\overrightarrow{AP}=(-1,\;\;0,\;\;\sqrt{3}),\;\;\overrightarrow{BE}=({-\frac{1}{2},\;\;-\frac{{\sqrt{3}}}{2},\;\;\frac{{\sqrt{3}}}{2}\;})$,
∴cos<$\overrightarrow{AP},\overrightarrow{BE}$>=|$\frac{\overrightarrow{AP}•\overrightarrow{BE}}{|\overrightarrow{AP}||\overrightarrow{BE}|}$|=|$\frac{-1×(-\frac{1}{2})+0×(-\frac{\sqrt{3}}{2})+\sqrt{3}×\frac{\sqrt{3}}{2}}{\sqrt{(-1)^{2}+(\sqrt{3})^{2}}×\sqrt{(-\frac{1}{2})^{2}+(-\frac{\sqrt{3}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}}$=$\frac{2\sqrt{7}}{7}$;
(3)解:由C,E,P三点共线,
得$\overrightarrow{DE}=λ\overrightarrow{DP}+(1-λ)\overrightarrow{DC}$,且0≤λ≤1,
从而有$\overrightarrow{DE}=(λ-1,\;\;\sqrt{3}(1-λ),\;\;\sqrt{3}λ),\;\;\overrightarrow{DB}=(0,\;\;\sqrt{3},\;\;0)$,
设平面EDB的法向量为$\overrightarrow n=(x,\;\;y,\;\;z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DB}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{(λ-1)x+\sqrt{3}(1-λ)y+\sqrt{3}λz=0}\\{\sqrt{3}y=0}\end{array}\right.$,
取x=$\sqrt{3}$,得$\overrightarrow n=({\sqrt{3},\;\;0,\;\;\frac{1-λ}{λ}})$,
又平面CBD的法向量可取$\overrightarrow m=(0,\;\;0,\;\;1)$,
∵二面角E-BD-C的大小为30°,∴cos30°=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{2}$|,解得$λ=\frac{1}{4}$.
∴$\overrightarrow{DE}=(-\frac{3}{4},\frac{3\sqrt{3}}{4},\frac{\sqrt{3}}{4})$,则|DE|=|$\overrightarrow{DE}$|=$\frac{\sqrt{39}}{4}$.
点评 本题考查平面与平面垂直的判定,考查了利用空间向量求解二面角的平面角,考查计算能力,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | 0或2 | B. | 2或$-\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com