
分析 根据反比例函数的图象和性质,可得当p为真时:m≤-7,根据恒成立转化为最值的原则,可得q为真时:m≤-6或m≥1,进而得到答案.
解答 解:∵命题p:$f(x)=\frac{2}{x-m}$在区间(m,+∞)是减函数,
故当p为真时:m≤-7,
a∈[-1,1]时,$\sqrt{{a}^{2}+8}$∈[2$\sqrt{2}$,3],
若不等式${m^2}+5m-3≥\sqrt{{a^2}+8}$对任意的实数a∈[-1,1]恒成立.
则m2+5m-3≥3,
解得:m≤-6或m≥1
故当q为真时:m≤-6或m≥1
若(?p)∧q为真命题,则m>-7,且m≤-6或m≥1
所以实数m的范围是-7<m≤-6或m≥1
点评 本题以命题的真假判断与应用为载体,考查了反比例函数的图象和性质,恒成立问题,难度中档.


科目:高中数学 来源: 题型:解答题
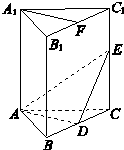 在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | B. | 函数f(x)是偶函数 | ||
| C. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | D. | 函数f(x)在区间$[0,\frac{π}{4}]$上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
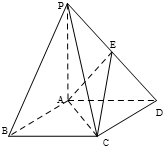 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PA=AB=2,BC=$\frac{1}{2}$PA,BD=$\sqrt{3}$,E在PC边上.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PA=AB=2,BC=$\frac{1}{2}$PA,BD=$\sqrt{3}$,E在PC边上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型①拟合效果好 | B. | 模型①与②的拟合效果一样好 | ||
| C. | 模型②拟合效果好 | D. | 模型①负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com