
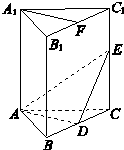
 在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.分析 (1)由ABC-A1B1C1是直三棱柱,得CC1⊥平面ABC,进一步得CC1⊥AD.又AD⊥DE,由线面垂直的判定得AD⊥平面BCC1B1.再由面面垂直的判定得平面ADE⊥平面BCC1B1;
(2)由A1B1=A1C1,F为B1C1的中点,得A1F⊥B1C1.进一步得CC1⊥A1F.可得A1F⊥平面BCC1B1.结合(1)知AD⊥平面BCC1B1,得A1F∥AD.再由线面平行的判定定理得A1F∥平面ADE;
(3)直接利用等积法把三棱锥F-ADE的体积转化为A-FDE的体积求解.
解答 (1)证明:∵ABC-A1B1C1是直三棱柱,∴CC1⊥平面ABC,
又AD?平面ABC,∴CC1⊥AD.
又∵AD⊥DE,CC1,DE?平面BCC1B1,CC1∩DE=E,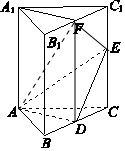
∴AD⊥平面BCC1B1.又AD?平面ADE,
∴平面ADE⊥平面BCC1B1;
(2)证明:∵A1B1=A1C1,F为B1C1的中点,∴A1F⊥B1C1.
∵CC1⊥平面A1B1C1,且A1F?平面A1B1C1,
∴CC1⊥A1F.
又∵CC1,B1C1?平面BCC1B1,CC1∩B1C1=C1,
∴A1F⊥平面BCC1B1.
由(1)知AD⊥平面BCC1B1,∴A1F∥AD.
又AD?平面ADE,A1F?平面ADE,∴A1F∥平面ADE;
(3)解:∵A1B1=A1C1=B1C1=2,∴AD=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
又A1A=4,∴${S}_{△FDE}=1×4-\frac{1}{2}×1×2-\frac{1}{2}×1×2=2$,
∴${V}_{F-ADE}={V}_{A-FDE}=\frac{1}{3}×2×\sqrt{3}=\frac{2\sqrt{3}}{3}$.
点评 本题考查直线与平面平行的判断,考查平面与平面垂直的判断,训练了利用等积法求多面体的体积,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $a<\frac{1}{3}$ | B. | $a≤\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a≥\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或2 | B. | 2或$-\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(1,2) | B. | (log37,2) | C. | (0,2) | D. | (0,1)∪(log37,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意两个复数均不能比较大小 | |
| B. | 复数z为实数的充要条件是$z=\overline z$ | |
| C. | 复数z=3+2i在复平面上对应的点在第二象限 | |
| D. | 复数i+3的共轭复数为i-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com