
| A. | $a<\frac{1}{3}$ | B. | $a≤\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a≥\frac{1}{3}$ |
分析 写出命题p的否定,求出f(x)=x3-3ax的导函数,得到导函数的范围,结合¬p为真可得关于a的不等式,则a的范围可求.
解答 解:由命题p:?b∈R,使直线y=-x+b是曲线y=x3-3ax的切线,得
?p:对任意的实数b,直线y=-x+b都不是曲线y=x3-3ax的切线.
由?p为真.
设f(x)=x3-3ax,求导函数,可得f′(x)=3x2-3a∈[-3a,+∞),
对任意的实数b,直线y=-x+b都不是曲线y=x3-3ax的切线,
∴-3a>-1,得a<$\frac{1}{3}$.
即实数a的取值范围为a$<\frac{1}{3}$.
故选:A.
点评 本题考查命题的真假判断与应用,考查学生会利用导数求曲线上过某点切线方程,考查直线的斜率与函数的导数的关系,考查计算能力,是中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ② | C. | ③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
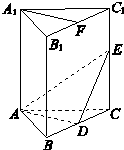 在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
在直三棱柱ABC-A1B1C1中,A1B1=A1C1=2,A1A=4,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com