
| A. | ①② | B. | ② | C. | ③ | D. | ①②③ |
分析 利用“折线距离”:d(A,B)=|x2-x1|+|y2-y1|,逐一判断命题①②③即可得到答案.
解答 解:①∵A(-1,3),B(1,0),则d(A,B)=|1-(-1)|+|0-3|=2+5=5,故①错误;
②不妨令点A为坐标原点,B(x,y),则d(A,B)=|x|+|y|=1,B点的轨迹是一个正方形,而不是圆,故②错误;
③设直角坐标平面内的任意两点A(x1,y1),B(x2,y2),设C点坐标为(x0,y0),
∵点C在线段AB上,
∴x0在x1、x2之间,y0在y1、y2之间,不妨令x1<x0<x2,y1<y0<y2,
则d(A,C)+d(C,B)=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|
=x0-x1+y0-y1+x2-x0+y2-y0
=x2-x1+y2-y1
=|x2-x1|+|y2-y1|
=d(A,B)成立,故③正确.
∴正确的命题是③.
故选:C.
点评 本题考查命题的真假判断与应用,着重考查创新思维与逻辑思维,考查等价转化思想与运算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 31 | C. | 33 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
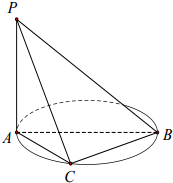 如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上异于A、B的点.
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上异于A、B的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a<\frac{1}{3}$ | B. | $a≤\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a≥\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若sinx=1,则$x≠\frac{π}{2}$ | B. | 存在sinx=1,使$x≠\frac{π}{2}$ | ||
| C. | 若sinx≠1,则$x≠\frac{π}{2}$ | D. | 若$x≠\frac{π}{2}$,则sinx≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com