Question

【题目】用秦九韶算法求多项式f（x）=7x7+6x6+5x5+4x4+3x3+2x2+x，当x=3时的值，并将结果化为8进制数．

Answer 1

【答案】解：f（x）=7x7+6x6+5x5+4x4+3x3+2x2+x=（（（（（（7x+6）x+5）x+4）x+3）x+2）x+1）x，
当x=3时的值，可得
v0=7，
v1=7×3+6=27，
v2=27×3+5=86，
v3=86×3+4=262，
v4=262×3+3=789，
v5=789×3+2=2369，
v6=2369×3+1=7108，
v7=7108×3=21324．
如图所示，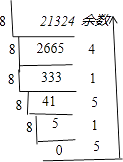

21324化为8进制数为51514（8） ．
【解析】利用f（x）=（（（（（（7x+6）x+5）x+4）x+3）x+2）x+1）x，可得f（3）=21324，再利用进位制的换算方法即可得出．
【考点精析】关于本题考查的秦九韶算法，需要了解求多项式的值时，首先计算最内层括号内依次多项式的值，即v1=anx+an-1然后由内向外逐层计算一次多项式的值，把n次多项式的求值问题转化成求n个一次多项式的值的问题才能得出正确答案．