考点:圆与圆锥曲线的综合,向量在几何中的应用,椭圆的标准方程
专题:计算题,转化思想
分析:(1)直接把椭圆经过点
(1,)的坐标代入方程,再结合焦点坐标即可求椭圆的方程;
(2)把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,再代入
•的表达式即可求出求
•的范围;
(3)先把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,求出
+,利用
+与向量
=(-2,1)共线求出直线斜率进而求出求
•的值及△AOB的外接圆方程.
解答:
解:(1)设椭圆方程为
+=1(a>b>0).
由题得
=1⇒a
2=2,b
2=1,
所以椭圆的方程是
+y2=1,
(2)当K存在时,设直线方程为y=K(x-1).
联立
,化简为(2k
2+1)x
2-4k
2x+2k
2-2=0
设A(x
1,y
1),B(x
2,y
2)
x1+ x2=,
x1•x2=.
•=x1x2+y1y2=x1x2+k2(x1-1) (x2-1)∴
• =
(#)
令
=m则
k2=≥0
∴
-2≤m<,∴
-2≤•<当K不存在时,
A(1,),B(1,-),则
•=
综上,-2≤
•≤
.
(3)
•=(x
1+x
2,y
1+y
2)
∴
-2(y1+y2)=x1+x2,
∴
-2(k(x1-1)+k(x2-1))=x1+x2由韦达定理知k=0或
k=代入(#)得
•=-2或0
当
•=-2时,A,O,B共线,不存在外接圆
当
•=0时,
⊥,外接圆直径为AB,圆心为
(,)即
(,-)r2=|OC|2=,
∴△AOB的外接圆方程为
(x-)2+(y+)2=.
点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.



 在港口
在港口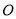 正东方
正东方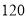 海里处,小岛
海里处,小岛 在港口
在港口 北偏东
北偏东 方向和港口
方向和港口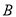 北偏西
北偏西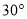 方向上,一艘科学考察船从港口O出发,沿北偏东
方向上,一艘科学考察船从港口O出发,沿北偏东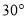 的
的 方向以每小时
方向以每小时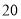 海里的速度驶离港口
海里的速度驶离港口 ,一艘快艇从港口B出发,以每小时
,一艘快艇从港口B出发,以每小时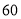 海里的速度驶向小岛
海里的速度驶向小岛 ,在
,在 岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要
岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要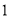 小时,问快艇驶离港口
小时,问快艇驶离港口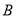 后最少要经过多少时间才能和考察船相遇?
后最少要经过多少时间才能和考察船相遇?