考点:数列与不等式的综合,数列的函数特性,数列的求和
专题:证明题
分析:(I)易知对任意n∈N
*,a
n>0,b
n>0.根据基本不等式可知对任意n∈N
*,a
n>b
n,
an+1-an=-an判定符号可得数列{a
n}的单调性,
bn+1-bn=-bn=(-)>0,从而得到数列{b
n}的单调性;
(II)根据题意可知
an+1-bn+1=-,然后利用放缩法即可证得结论;
(III)根据(II)可得
an-bn<(a-b)•()n-1,从而
,最后利用放缩法即可证得结论.
解答:
(Ⅰ)证明:易知对任意n∈N
*,a
n>0,b
n>0.
由a≠b,可知
>,即a
1>b
1.
同理,
>,即a
2>b
2.
可知对任意n∈N
*,a
n>b
n.
an+1-an=-an=<0,
所以数列{a
n}是递减数列.
bn+1-bn=-bn=(-)>0,
所以数列{b
n}是递增数列. …(5分)
(Ⅱ)证明:
an+1-bn+1=-<-<(an-bn).…(10分)
(Ⅲ)解:由
an+1-bn+1<(an-bn),可得
an-bn<(a-b)•()n-1.
| | Sn-Tn<(a+b)(1++…+()n-1). | | <(a+b)(2-()n)<2(a-b) |
| |
∴S
n<T
n+2(a+b).…(14分)
点评:本题主要考查了数列的单调性的判定,以及利用放缩法证明不等式,同时考查了计算能力,属于中档题.



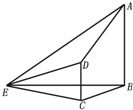 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.