解:(1)任取1<x
1<x
2,则
f(x
2)-f(x
1)=log
a
-log
a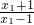
=log
a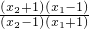
=log
a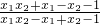
.
又∵x
2>x
1>1,∴x
1-x
2<x
2-x
1.
∴0<x
1x
2-x
2+x
1-1<x
1x
2-x
1+x
2-1.
∴0<
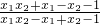
<1.
当a>1时,f(x
2)-f(x
1)<0,
∴f(x)在(1,+∞)上是减函数;
当0<a<1时,f(x
2)-f(x
1)>0,
∴f(x)在(1,+∞)上是增函数.
(2)由

>0得x∈(-∞,-1)∪(1,+∞).
∵

=1+

≠1,∴f(x)≠0.
当a>1时,
∵x>1?f(x)>0,x<-1?f(x)<0,
∴要使f(x)的值域是(1,+∞),只有x>1.
又∵f(x)在(1,+∞)上是减函数,
∴f
-1(x)在(1,+∞)上也是减函数.
∴f(x)>1?1<x<f
-1(1)=
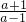
.
∴
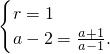
∴

当0<a<1时,
∵x>1?f(x)<0,x<-1?f(x)>0,
∴要使值域是(1,+∞),只有x<-1.
又∵f(x)在(-∞,-1)上是增函数,
∴f(x)>1?-1>x>f
-1(1)=
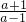
.
∴
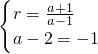
无解.
综上,得a=2+

,r=1.
(3)由f(x)≥log
a2x得
当a>1时,
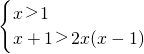
?
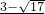
<x<

且x>1.
∴1<x<

.
当0<a<1时,
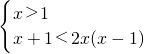
∴x>

.
分析:(1)利用函数单调性的定义,通过对a分类讨论判断出f(x)的单调性.
(2)求出函数的定义域,对a分类讨论求函数的值域;利用原函数与其反函数的关系列出方程,求出a与r.
(3)对a分类讨论,利用函数的单调性脱去对数符号,解不等式组求出解集.
点评:本题考查函数单调性的定义、原函数与反函数的关系、利用对数函数的单调性解对数不等式、分类讨论的数学思想.

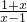 (a>0,a≠1).
(a>0,a≠1). -loga
-loga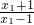
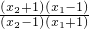
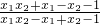 .
.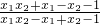 <1.
<1. >0得x∈(-∞,-1)∪(1,+∞).
>0得x∈(-∞,-1)∪(1,+∞). =1+
=1+ ≠1,∴f(x)≠0.
≠1,∴f(x)≠0.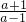 .
.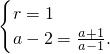 ∴
∴
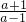 .
.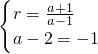 无解.
无解. ,r=1.
,r=1.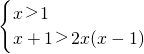 ?
?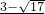 <x<
<x< 且x>1.
且x>1. .
.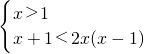
 .
.
