
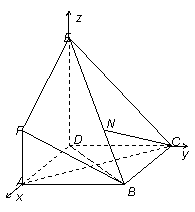
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.
(1)证明: BE⊥AC;
(2)在棱BE上是否存在一点N,,使得直线CN与平面ADE成30°角,若存在,求出BN的长度:若不存在,说明理由。

解:(Ⅰ)法一:连结BD,∵ABCD是正方形,
 ∴BD⊥AC. - ∵AF⊥平面ABCD,DE∥AF,
∴BD⊥AC. - ∵AF⊥平面ABCD,DE∥AF,
∴DE⊥平面ABCD,
∴DE⊥AC,
∵BD 、DE在平面BDE内,且相交于D,
∴AC⊥平面BDE,
∴BE⊥AC.
法二:∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,
∴A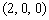 ,C
,C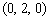 ,B
,B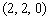 ,E
,E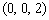 ,
,
∴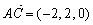 ,
,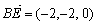 ,
,
∵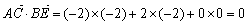 ,∴
,∴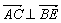 ,即BE⊥AC.
,即BE⊥AC.
(Ⅱ)∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,
∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,
∴B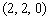 ,C
,C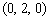 , E
, E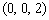 ,D
,D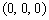 ,
,
∴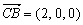 ,
,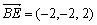 ,
,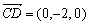 ,
,
∵点N在棱BE上,∴可设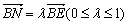 ,
,
∴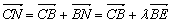 =
=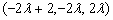 ,
,
由于CD⊥平面ADE,∴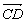 为平面ADE的法向量.
为平面ADE的法向量.
当直线CN与平面ADE成30°角时, 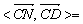 60°,
60°,
∴ 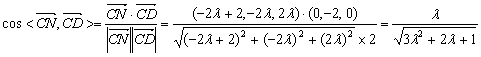 ,
,
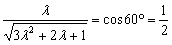 ,解得
,解得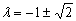 ,∵
,∵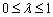 ,∴
,∴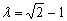 ,---12分
,---12分
∴BN=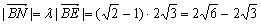 . 4
. 4


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
下列命题中错误的是 ( )
A.如果平面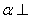 平面
平面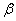 ,那么平面
,那么平面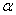 内一定存在直线平行于平面
内一定存在直线平行于平面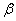
B.如果平面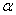 不垂直于平面
不垂直于平面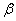 ,那么平面
,那么平面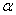 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面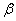
C.如果平面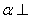 平面
平面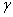 ,平面
,平面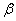 ⊥平面
⊥平面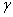 ,
,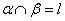 ,那么
,那么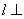 平面
平面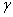
D.如果平面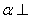 平面
平面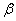 ,那么平面
,那么平面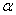 内有且只有一条直线垂直于平面
内有且只有一条直线垂直于平面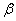
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com