
【题目】已知点![]() 在圆
在圆![]()
![]() 上,点在圆
上,点在圆![]()
![]() 上,则下列说法错误的是
上,则下列说法错误的是
A. ![]() 的取值范围为
的取值范围为![]()
B. ![]() 取值范围为
取值范围为![]()
C. ![]() 的取值范围为
的取值范围为![]()
D. 若![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为![]()
【答案】B
【解析】∵M在圆C1上,点N在圆C2上,
∴∠MON≥90°,
∴![]() ≤0,
≤0,
又OM≤![]() +1,ON≤
+1,ON≤![]() +1,
+1,
∴当OM=![]() +1,ON=
+1,ON=![]() +1时,
+1时,
![]() 取得最小值(
取得最小值(![]() +1)2cosπ=﹣3﹣2
+1)2cosπ=﹣3﹣2![]() ,故A正确;
,故A正确;
设M(1+cosα,1+sinα),
N(﹣1+cosβ,﹣1+sinβ),
则![]() =(cosα+cosβ,sinα+sinβ),
=(cosα+cosβ,sinα+sinβ),
∴![]() 2=2cosαcosβ+2sinαsinβ+2=2cos(α﹣β)+2,
2=2cosαcosβ+2sinαsinβ+2=2cos(α﹣β)+2,
∴0≤![]() ≤2,故B错误;
≤2,故B错误;
∵两圆外离,半径均为1,|C1C2|=2![]() ,
,
∴2![]() ﹣2≤|MN|≤2
﹣2≤|MN|≤2![]() +2,即2
+2,即2![]() ﹣2≤
﹣2≤![]() ≤2
≤2![]() +2,故C正确;
+2,故C正确;
∵![]() ﹣1≤|OM|≤
﹣1≤|OM|≤![]() +1,
+1,![]() -1≤|ON|≤
-1≤|ON|≤![]() +1,
+1,
∴当![]() 时,
时,![]() ≤﹣λ≤
≤﹣λ≤![]() ,解得﹣3﹣2
,解得﹣3﹣2![]() ≤λ≤﹣3+2
≤λ≤﹣3+2![]() ,故D正确.
,故D正确.
故选B.
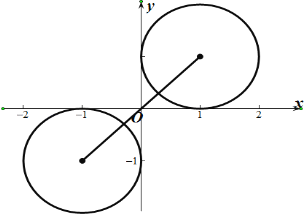


科目:高中数学 来源: 题型:
【题目】已知向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(sin(x﹣
=(sin(x﹣![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2![]()
![]() ,g(x)=f(
,g(x)=f(![]() ).
).
(1)求f(x)在[![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代数学名著《九章算术》中的“盈不足”问题知两鼠穿垣.今有垣厚5尺,两鼠对穿.大鼠日一尺,小鼠亦一尺.大鼠日自倍,小鼠日自半.问:何日相逢?题意是:由垛厚五尺(旧制长度单位, ![]() 尺=
尺= ![]() 寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进
寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进![]() 尺,以后每天的速度为前一天的
尺,以后每天的速度为前一天的![]() 倍;小鼠第一天也打进
倍;小鼠第一天也打进![]() 尺,以后每天的进度是前一天的一半.它们多久可以相遇?
尺,以后每天的进度是前一天的一半.它们多久可以相遇?
A. ![]() 天 B.
天 B. ![]() 天 C.
天 C. ![]() 天 D.
天 D. ![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为
轴上截得的弦长为![]() ,记动圆圆心的轨迹为曲线
,记动圆圆心的轨迹为曲线![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 围成的区域面积;
围成的区域面积;
(2)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。设![]() 表示前
表示前![]() 年的纯收入(
年的纯收入(![]() 前
前![]() 年的总收入一前
年的总收入一前![]() 年的总支出一投资额)
年的总支出一投资额)
(1)试写出![]() 的关系式.
的关系式.
(2) 该开发商从第几年开始获利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A在直线2x-3y+5=0上移动,点P为连接M(4,-3)和点A的线段的中点,则点P的轨迹方程为
A. 2x-3y-6=0 B. 2x-3y+2=0 C. 2x-3y+11=0 D. 2x+3y-6=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数, ![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com