
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
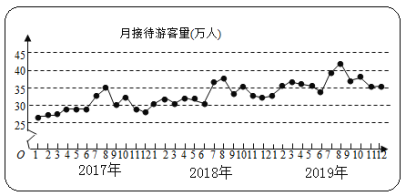
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】踢毽子是中国民间传统的运动项目之一,起源于汉朝,至今已有两千多年的历史,是一项简便易行的健身活动.某单位组织踢毽子比赛,把10人平均分成甲、乙两组,其中甲组每人在1分钟内踢毽子的数目分别为26,29,32,45,51;乙组每人在1分钟内踢毽子的数目分别为28,31,38,42,49.从甲、乙两组中各随机抽取1人,则这两人踢毽子的数目之和为奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
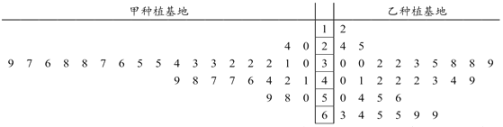
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,①已知点
中,①已知点![]() ,直线
,直线![]() :
:![]() ,动点
,动点![]() 满足到点
满足到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ;②已知圆
;②已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 为圆
为圆![]() 的切线,记点
的切线,记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,动点
,动点![]() 满足
满足![]() ;③点
;③点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,且
轴上运动,且![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)在①,②,③这三个条件中任选一个,求动点![]() 的轨迹方程;
的轨迹方程;
(2)记(1)中的轨迹为![]() ,经过点
,经过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求点
,求点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,
,![]() ,记数列
,记数列![]() 的前n项和是
的前n项和是![]() ,则( )
,则( )
A.若数列![]() 是常数列,则
是常数列,则![]()
B.若![]() ,则数列
,则数列![]() 单调递减
单调递减
C.若![]() ,则
,则![]()
D.若![]() ,任取
,任取![]() 中的9项
中的9项![]() 构成数列
构成数列![]() 的子数列
的子数列![]() ,则
,则![]() 不全是单调数列
不全是单调数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右两个焦点为
的左,右两个焦点为![]() 、
、![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有公共焦点
有公共焦点![]() .且两曲线
.且两曲线![]() 、
、![]() 在第一象限的交点
在第一象限的交点![]() 的横坐标为
的横坐标为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 为坐标原点),与椭圆
为坐标原点),与椭圆![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 在线段
在线段![]() 上),且
上),且![]() .问满足条件的直线
.问满足条件的直线![]() 有几条,说明理由.
有几条,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
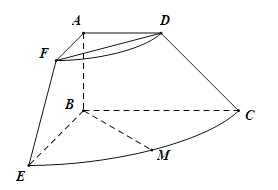
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com