
【题目】若数列![]() 满足
满足![]() ,
,![]() ,记数列
,记数列![]() 的前n项和是
的前n项和是![]() ,则( )
,则( )
A.若数列![]() 是常数列,则
是常数列,则![]()
B.若![]() ,则数列
,则数列![]() 单调递减
单调递减
C.若![]() ,则
,则![]()
D.若![]() ,任取
,任取![]() 中的9项
中的9项![]() 构成数列
构成数列![]() 的子数列
的子数列![]() ,则
,则![]() 不全是单调数列
不全是单调数列
【答案】C
【解析】
对于A:由数列![]() 为常数数列,则
为常数数列,则![]() ,解方程可得
,解方程可得![]() 的值;
的值;
对于B:由函数![]() ,
,![]() ,求得导数,判断单调性和极值,即可进行判断;
,求得导数,判断单调性和极值,即可进行判断;
对于D:由![]() ,判断
,判断![]() 的奇偶性和单调性,结合正弦函数的单调性,可得数列
的奇偶性和单调性,结合正弦函数的单调性,可得数列![]() 都是单调数列,即可进行判断.
都是单调数列,即可进行判断.
对于A:若数列![]() 为常数列,则
为常数列,则![]() ,
,![]() 或
或![]() ,故A错误;
,故A错误;
对于B:若![]() ,
,![]() ,
,![]() ,设函数
,设函数![]() ,
,![]() ,由
,由![]() ,可得极值点唯一且为
,可得极值点唯一且为![]() ,极值点为
,极值点为![]() ,
,
由![]() ,可得
,可得![]() ,
,
则![]() ,即有
,即有![]()
由于![]() ,
,![]() ,由正弦函数单调性可得
,由正弦函数单调性可得![]() ,
,
所以数列![]() 是单调递增函数,故B错误;
是单调递增函数,故B错误;
对于D:若![]() ,任取
,任取![]() 中的9项
中的9项![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
构成数列![]() 的子数列
的子数列![]() ,
,![]() ,2,
,2,![]() ,9,
,9,![]() 是单调递增数列;
是单调递增数列;
由![]() ,可得
,可得![]() ,
,![]() 为奇函数;
为奇函数;
当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
运用正弦函数的单调性可得![]() 或
或![]() 时,数列
时,数列![]() 单调递增;
单调递增;
![]() 或
或![]() 时,数列
时,数列![]() 单调递减.
单调递减.
所以数列![]() 都是单调数列,故D错误;
都是单调数列,故D错误;
故选C.


科目:高中数学 来源: 题型:
【题目】某公司为加强对销售员的考核与管理,从销售部门随机抽取了2019年度某一销售小组的月均销售额,该小组各组员2019年度的月均销售额(单位:万元)分别为:3.35,3.35,3.38,3.41,3.43,3.44,3.46,3.48,3.51,3.54,3.56,3.56,3.57,3.59,3.60,3.64,3.64,3.67,3.70,3.70.
(Ⅰ)根据公司人力资源部门的要求,若月均销售额超过3.52万元的组员不低于全组人数的![]() ,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
,则对该销售小组给予奖励,否则不予奖励.试判断该公司是否需要对抽取的销售小组发放奖励;
(Ⅱ)从该销售小组月均销售额超过3.60万元的销售员中随机抽取2名组员,求选取的2名组员中至少有1名月均销售额超过3.68万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,点A,B的坐标分别为![]() ,
,![]() ,P是坐标平面内的动点,且直线
,P是坐标平面内的动点,且直线![]() ,
,![]() 的斜率之积等于
的斜率之积等于![]() .设点P的轨迹为C.
.设点P的轨迹为C.
(1)求轨迹C的方程;
(2)某同学对轨迹C的性质进行探究后发现:若过点![]() 且倾斜角不为0的直线
且倾斜角不为0的直线![]() 与轨迹C相交于M,N两点,则直线
与轨迹C相交于M,N两点,则直线![]() ,
,![]() 的交点Q在一条定直线上.此结论是否正确?若正确,请给予证明,并求出定直线方程;若不正确,请说明理由.
的交点Q在一条定直线上.此结论是否正确?若正确,请给予证明,并求出定直线方程;若不正确,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为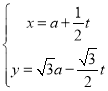 (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点、
).在以坐标原点为极点、![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人坚持跑步锻炼,根据他最近20周的跑步数据,制成如下条形图:
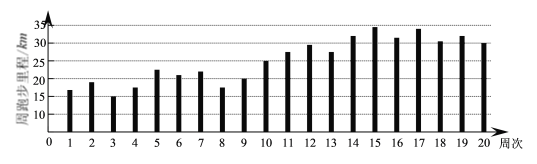
根据条形图判断,下列结论正确的是( )
A.周跑步里程逐渐增加
B.这20周跑步里程平均数大于30km
C.这20周跑步里程中位数大于30km
D.前10周的周跑步里程的极差大于后10周的周跑步里程的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
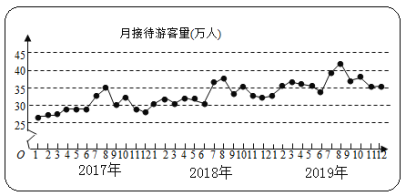
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式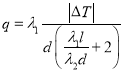 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日,武汉市雷神山医院为确诊新型冠状病毒肺炎患者,需要检测核酸是否为阳性,现有![]() 份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测
份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测![]() 次;(2)混合检测,将其中
次;(2)混合检测,将其中![]() (
(![]() ,且
,且![]() )份核酸样本分别取样混合在一起检测,若检测结果为阴性,这
)份核酸样本分别取样混合在一起检测,若检测结果为阴性,这![]() 份核酸样本全为阴性,因而这
份核酸样本全为阴性,因而这![]() 份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这
份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这![]() 份核酸样本究竟哪几份为阳性,就要对这
份核酸样本究竟哪几份为阳性,就要对这![]() 份样本再逐份检测,此时这
份样本再逐份检测,此时这![]() 份核酸样本的检测次数总共为
份核酸样本的检测次数总共为![]() 次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份核酸样本,其中只有2份样本为阳性,若采用逐份检测方式,求恰好经过4次检测就能把阳性样本全部检测出来的概率.
(2)现取其中![]() (
(![]() ,且
,且![]() )份核酸样本,记采用逐份检测方式,样本需要检测的总次数为
)份核酸样本,记采用逐份检测方式,样本需要检测的总次数为![]() ,采用混合检测方式,样本需要检测的总次数为
,采用混合检测方式,样本需要检测的总次数为![]() .
.
①试运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求
,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com