
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
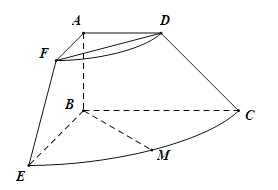
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
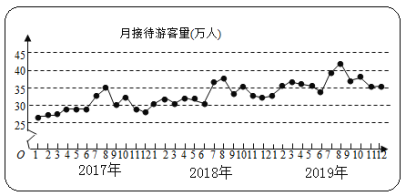
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
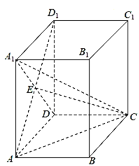
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
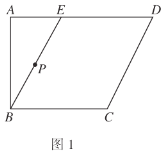
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.
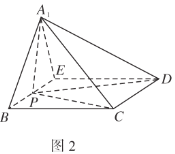
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,当直线
上,当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日,武汉市雷神山医院为确诊新型冠状病毒肺炎患者,需要检测核酸是否为阳性,现有![]() 份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测
份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测![]() 次;(2)混合检测,将其中
次;(2)混合检测,将其中![]() (
(![]() ,且
,且![]() )份核酸样本分别取样混合在一起检测,若检测结果为阴性,这
)份核酸样本分别取样混合在一起检测,若检测结果为阴性,这![]() 份核酸样本全为阴性,因而这
份核酸样本全为阴性,因而这![]() 份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这
份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这![]() 份核酸样本究竟哪几份为阳性,就要对这
份核酸样本究竟哪几份为阳性,就要对这![]() 份样本再逐份检测,此时这
份样本再逐份检测,此时这![]() 份核酸样本的检测次数总共为
份核酸样本的检测次数总共为![]() 次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份核酸样本,其中只有2份样本为阳性,若采用逐份检测方式,求恰好经过4次检测就能把阳性样本全部检测出来的概率.
(2)现取其中![]() (
(![]() ,且
,且![]() )份核酸样本,记采用逐份检测方式,样本需要检测的总次数为
)份核酸样本,记采用逐份检测方式,样本需要检测的总次数为![]() ,采用混合检测方式,样本需要检测的总次数为
,采用混合检测方式,样本需要检测的总次数为![]() .
.
①试运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求
,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学、跑步、骑行、交友及健身饮食指导、装备购买等一站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程.不仅如此,它还可以根据不同人的体质,制定不同的健身计划.小明根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.根据该折线图,下列结论正确的是( )
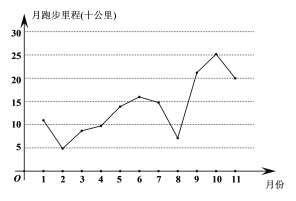
A.月跑步里程最小值出现在2月
B.月跑步里程逐月增加
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目:高中数学 来源: 题型:
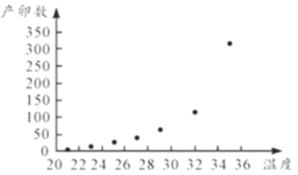
【题目】从![]() 年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数
年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数![]() 和平均温度
和平均温度![]() 有关,现收集了以往某地的
有关,现收集了以往某地的![]() 组数据,得到下面的散点图及一些统计量的值.
组数据,得到下面的散点图及一些统计量的值.
平均温度 |
|
|
|
|
|
|
|
平均产卵数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数![]() 关于平均温度
关于平均温度![]() 的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出![]() 关于
关于![]() 的回归方程.(结果精确到小数点后第三位)
的回归方程.(结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到![]() 以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到
以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到![]() 以上的概率为
以上的概率为![]() .
.
①记该地今后![]() 年中,恰好需要
年中,恰好需要![]() 次人工防治的概率为
次人工防治的概率为![]() ,求
,求![]() 取得最大值时相应的概率
取得最大值时相应的概率![]() ;
;
②根据①中的结论,当![]() 取最大值时,记该地今后
取最大值时,记该地今后![]() 年中,需要人工防治的次数为
年中,需要人工防治的次数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新冠病毒疫情爆发期间,口罩成为了个人的必需品.已知某药店有4种不同类型的口罩![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 型口罩仅剩1只(其余3种库存足够).今甲、乙等5人先后在该药店各购买了1只口罩,统计发现他们恰好购买了3种不同类型的口罩,则所有可能的购买方式共有( )
型口罩仅剩1只(其余3种库存足够).今甲、乙等5人先后在该药店各购买了1只口罩,统计发现他们恰好购买了3种不同类型的口罩,则所有可能的购买方式共有( )
A.330种B.345种C.360种D.375种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于由正整数构成的数列![]() ,若对任意
,若对任意![]() ,
,![]() “且
“且![]() ,
,![]() 也是
也是![]() 中的项,则称
中的项,则称![]() 为
为![]() 数列”.设数列
数列”.设数列![]() |满足
|满足![]() ,
,![]() ..
..
(1)请给出一个![]() 的通项公式,使得
的通项公式,使得![]() 既是等差数列也是“
既是等差数列也是“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)根据你给出的通项公式,设![]() 的前
的前![]() 项和为
项和为![]() ,求满足
,求满足![]() 的正整数
的正整数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com