练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
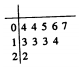
    11．某公司10个部门在公司20周年庆典中获奖人数如茎叶图所示，则这10个部门获奖人数的中位数和众数分别为（　　）
    A．10，13B．7，13C．10，4D．13，10

    分析 根据茎叶图写出这组数据，把数据按照从大到小排列，最中间的一个或最中间两个数字的平均数就是中位数，根据众数是出现次数最多的数求出众数．

    解答 解：由茎叶图可知：
    这组数据为4，4，5，6，7，13，13，13，14，22，
    所以其中位数为$\frac{7+13}{2}$=10，
    由茎叶图知出现次数最多的数是13，可得众数为13．
    故选：A．

    点评 本题利用茎叶图考查了中位数与众数的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．某天将一枚硬币连掷了10次，正面朝上的情形出现了6次，若用A表示正面朝上这一事件，则A的（　　）
    A．概率为$\frac{3}{5}$B．频率为$\frac{3}{5}$C．频率为6D．概率接近0.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．关于x的方程x2+2（m+1）x+2m+6=0有两个实根，一个比2大，一个比2小，则实数m的范围为m＜-$\frac{7}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．《张邱建算经》是我国古代数学著作大约创作于公元五世纪．书中有如下问题：“今有女善织，日益功疾，初日织五尺，今一月，日织九匹三丈，问日益几何？”该题大意是：“一女子擅长织布，一天比一天织的快，而且每天增加的量都一样，已知第一天织了5尺，一个月后，共织布390尺，问该女子每天增加$\frac{16}{29}$尺．（一月按30天计）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

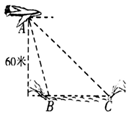    6．某人要利用无人机测量河流的宽度，如图，从无人机A处测得正前方河流的两岸B，C的俯角分别为75°，30°，此时无人机的高是60米，则河流的宽度BC等于（　　）
    A．$240\sqrt{3}$米B．$180（\sqrt{2}-1）$米C．$120（\sqrt{3}-1）$米D．$30（\sqrt{3}+1）$米

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若圆C：（x-5）2+（y+1）2=m（m＞0）上有且只有一点到直线4x+3y-2=0的距离为1，则实数m的值为（　　）
    A．4B．16C．4或16D．2或4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某公司2016年前三个月的利润（单位：百万元）如表：
    月份123
    利润23.95.5
    （1）求利润y关于月份x的线性回归方程；
    （2）试用（1）中求得的回归方程预测4月和5月的利润；
    （3）试用（1）中求得的回归方程预测该公司2016年从几月份开始利润超过1000万？
    相关公式：b=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata$=$\overline y$-$\widehatb\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知函数f（x）=2x-1+a，g（x）=bf（1-x），其中a，b∈R，若关于x的不等式f（x）≥g（x）的解的最小值为2，则实数a的取值范围是a≤-2或a＞-$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．函数y=x2-2x-1（-2≤x≤2）的值域为[-2，7]．

    查看答案和解析>>

    同步练习册答案