
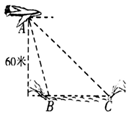
 某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )
某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )| A. | $240\sqrt{3}$米 | B. | $180(\sqrt{2}-1)$米 | C. | $120(\sqrt{3}-1)$米 | D. | $30(\sqrt{3}+1)$米 |
分析 由题意画出图形,由两角差的正切求出15°的正切值,然后通过求解两个直角三角形得到DC和DB的长度,作差后可得答案.
解答 解:如图
由图可知,∠DAB=15°,
∵tan15°=tan(45°-30°)=2-$\sqrt{3}$.
在Rt△ADB中,又AD=60,
∴DB=AD•tan15°=60×(2-$\sqrt{3}$)=120-60$\sqrt{3}$.
在Rt△ADC中,∠DAC=60°,AD=60,
∴DC=AD•tan60°=60$\sqrt{3}$.
∴BC=DC-DB=60$\sqrt{3}$-(120-60$\sqrt{3}$)=120($\sqrt{3}$-1)(m).
∴河流的宽度BC等于120($\sqrt{3}$-1)m.
故选:C.
点评 本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {y|y=1或2} | ||
| C. | $\{(x,y)|\left\{{\begin{array}{l}{x=0}\\{y=1}\end{array}}\right.$或$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$} | D. | {y|y≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
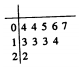 某公司10个部门在公司20周年庆典中获奖人数如茎叶图所示,则这10个部门获奖人数的中位数和众数分别为( )
某公司10个部门在公司20周年庆典中获奖人数如茎叶图所示,则这10个部门获奖人数的中位数和众数分别为( )| A. | 10,13 | B. | 7,13 | C. | 10,4 | D. | 13,10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com