
分析 由题意根据平移变换求出函数的解析式,然后即可代入求值得解.
解答 解:函数f(x)=$6sin({2x-\frac{π}{3}})$的图象向右平移$\frac{π}{12}$个单位,
则函数变为g(x)=6sin[2(x-$\frac{π}{12}$)-$\frac{π}{3}$]=6sin(2x-$\frac{π}{2}$)=-6cos2x;
可得:$g({\frac{π}{12}})$=-6cos(2×$\frac{π}{12}$)=-6cos$\frac{π}{6}$=$-3\sqrt{3}$
故答案为:$-3\sqrt{3}$.
点评 本题考查三角函数图象的平移变换,考查计算能力,逻辑推理能力,常考题型,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
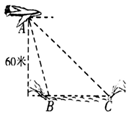 某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )
某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )| A. | $240\sqrt{3}$米 | B. | $180(\sqrt{2}-1)$米 | C. | $120(\sqrt{3}-1)$米 | D. | $30(\sqrt{3}+1)$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份 | 1 | 2 | 3 |
| 利润 | 2 | 3.9 | 5.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com