
分析 作出不等式对应的平面区域,利用线性规划的知识先求出a,b的关系,然后利用基本不等式求$\frac{3}{a}+\frac{4}{b}$的最小值.
解答 解:由z=ax+by(a>0,b>0)得y=$-\frac{a}{b}x+\frac{z}{b}$,
作出可行域如图: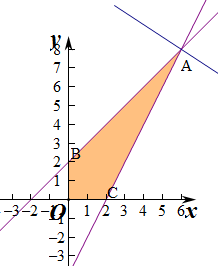
∵a>0,b>0,
∴直线y=$-\frac{a}{b}x+\frac{z}{b}$的斜率为负,且截距最大时,z也最大.
平移直线y=$-\frac{a}{b}x+\frac{z}{b}$,由图象可知当y=$-\frac{a}{b}x+\frac{z}{b}$经过点A时,
直线的截距最大,此时z也最大.
由$\left\{\begin{array}{l}{x-y+2=0}\\{2x-y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=6}\\{y=8}\end{array}\right.$,即A(6,8).
此时z=6a+8b=12,
即$\frac{a}{2}$+$\frac{2b}{3}$=1,
则$\frac{3}{a}+\frac{4}{b}$=($\frac{3}{a}+\frac{4}{b}$)($\frac{a}{2}$+$\frac{2b}{3}$)
=$\frac{3}{2}$+$\frac{8}{3}$+$\frac{2b}{a}$+$\frac{2a}{b}$≥$\frac{25}{6}$+2$\sqrt{\frac{2b}{a}•\frac{2a}{b}}$=$\frac{25}{6}$+4=$\frac{49}{6}$,
当且仅当$\frac{2b}{a}$=$\frac{2a}{b}$时取=号,
故答案为:$\frac{49}{6}$
点评 本题主要考查线性规划的应用以及基本不等式的应用,利用数形结合是解决线性规划题目的常用方法.


科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{2}$] | B. | (-1,$\frac{1}{2}$] | C. | [1,+∞) | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | (-∞,0)∪(4,+∞) | C. | (0,4) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知x,y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,z=2x-y
已知x,y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,z=2x-y查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 概率为$\frac{3}{5}$ | B. | 频率为$\frac{3}{5}$ | C. | 频率为6 | D. | 概率接近0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={({\frac{3}{2}})^x}$ | C. | $y={log_{\frac{3}{2}}}x$ | D. | y=-2x2+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
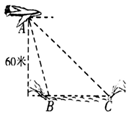 某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )
某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( )| A. | $240\sqrt{3}$米 | B. | $180(\sqrt{2}-1)$米 | C. | $120(\sqrt{3}-1)$米 | D. | $30(\sqrt{3}+1)$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com