
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={({\frac{3}{2}})^x}$ | C. | $y={log_{\frac{3}{2}}}x$ | D. | y=-2x2+3 |
分析 根据指数函数,对数函数,幂函数,二次函数的图象和性质,分析函数的单调性和奇偶性,可得答案.
解答 解:函数$y={x^{\frac{2}{3}}}$是偶函数,由y′=$\frac{2}{3}{x}^{-\frac{1}{3}}$>0在(0,+∞)恒成立,可得函数在(0,+∞)上为增函数,
函数$y={({\frac{3}{2}})^x}$是非奇非偶函数,
函数$y={log_{\frac{3}{2}}}x$是非奇非偶函数,
函数y=-2x2+3偶函数,由y′=-4x<0在(0,+∞)恒成立,可得函数在(0,+∞)上为减函数,
故选:A.
点评 本题考查的知识点是函数的单调性的判断与证明,函数的奇偶性,利用导数研究函数的单调性,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
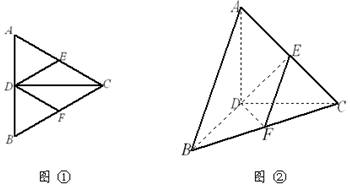 已知如图①,正三角形ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②.
已知如图①,正三角形ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (0,1) | C. | (1,3] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {y|y=1或2} | ||
| C. | $\{(x,y)|\left\{{\begin{array}{l}{x=0}\\{y=1}\end{array}}\right.$或$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$} | D. | {y|y≥1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com