
分析 (1)由已知得k(x+1)≥k2+2x-4,由k=2,k>2,k<2且k≠0,分类讨论,求出不等式的解集,再由2∈{x|$\frac{x+1}{k}$≥1+$\frac{2x-4}{{k}^{2}}$},能求出实数k的取值范围.
(2)由k=2,k>2,k<2且k≠0,分类讨论,求出不等式的解集,从而得到集合A.
解答 解:(1)∵关于x的不等式:$\frac{x+1}{k}$≥1+$\frac{2x-4}{{k}^{2}}$的解集为A,且2∈A,
∵$\frac{x+1}{k}$≥1+$\frac{2x-4}{{k}^{2}}$,∴k(x+1)≥k2+2x-4,
∴(k-2)x≥k2-k-4,
∴①当k=2时,不等式的解集为R;
②当k>2时,不等式的解为x≥$\frac{{k}^{2}-k-4}{k-2}$,即解集为:[$\frac{{k}^{2}-k-4}{k-2}$,+∞);
③当k<2且k≠0时,不等式的解为x≤$\frac{{k}^{2}-k-4}{k-2}$,即解集为(-∞,$\frac{{k}^{2}-k-4}{k-2}$]
∵2∈A,∴2∈{x|$\frac{x+1}{k}$≥1+$\frac{2x-4}{{k}^{2}}$},
∴k=2符合,
当k>2时,$\left\{\begin{array}{l}{k>2}\\{2≥\frac{{k}^{2}-k-4}{k-2}}\end{array}\right.$,解得2<k<3;
当k<2时,$\left\{\begin{array}{l}{k<2}\\{2≤\frac{{k}^{2}-k-4}{k-2}}\end{array}\right.$,解得0<k<2.
综上,实数k的取值范围是(0,3).
(2)由(1)得,当k=2时,A=R;
当k>2时,A=[$\frac{{k}^{2}-k-4}{k-2}$,+∞);
当k<2且k≠0时,A=(-∞,$\frac{{k}^{2}-k-4}{k-2}$].
点评 本题考查含参不等式的解法,考查分类讨论思想、等价转化思想的运用,考查运算能力、论证求解能力的培养,是中档题和易错题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{5}$,$\sqrt{5}$] | B. | (-1,1) | C. | (-1,$\sqrt{5}$] | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
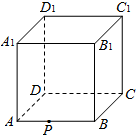 如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )
如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com