【题目】已知由实数组成的等比数列{an}的前项和为Sn ， 且满足8a4=a7 ， S7=254．
（1）求数列{an}的通项公式；
（2）对n∈N* ， bn= 
，求数列{bn}的前n项和Tn ．
每课必练系列答案
巧学巧练系列答案科目：高中数学 来源： 题型：
【题目】如图所示，已知多面体
中，四边形
为矩形， 
， 
，平面
平面
， 
、
分别为
、
的中点．
（
）求证： 
．
（
）求证： 
平面
．
（
）若过
的平面交
于点
，交
于
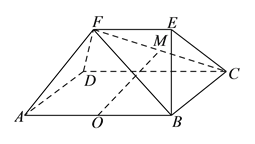
，求证： 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（e为自然对数的底）．若函数g（x）=f（x）﹣kx恰好有两个零点，则实数k的取值范围是（ ）
A.（1，e）
B.（e，10]
C.（1，10]
D.（10，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点，M为平面上任一点，A，B，C三点满足
．
（1）求
的值；
（2）已知A(1,sinx)、B(1+sinx,sinx)，M(1+
sinx,sinx)，x∈(0,π)，且函数
的最小值为
，求实数m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度
（单位：千米/小时）是车流密度
（单位：辆/千米）
的函数．当桥上的车流密度达到200辆/千米时，就会造成堵塞，此时车流速度为0；当
车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
时，
车流速度
是车流密度
的一次函数．
（1）当
时，求函数
的表达式；
（2）如果车流量（单位时间内通过桥上某观测点的车辆数）
(单位：辆/小时）,那么当车流密度
为多大时，车流量
可以达到最大，并求出最大值．（精确到
辆/小时）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中是真命题的是（ ）
①“若x2＋y2≠0，则x，y不全为零”的否命题 ②“正多边形都相似”的逆命题
③“若m>0，则x2＋x－m=0有实根”的逆否命题④“若x－
是有理数，则x是
无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列结论不正确的是________（填序号）.
①各个面都是三角形的几何体是三棱锥；
②以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥；
③棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥；
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点.
(1)求证：PA⊥BD；
(2)求证：平面BDE⊥平面PAC；
(3)当PA∥平面BDE时，求三棱锥E－BCD的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
