练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知数列{an}是等差数列，且a4=1，a7=16，则a6等于（　　）
    A．9B．10C．11D．12

    分析 由等差数列的通项公式列出方程组，求出首项和公差，由此能求出a6．

    解答 解：∵数列{an}是等差数列，且a4=1，a7=16，
    ∴$\left\{\begin{array}{l}{{a}_{4}={a}_{1}+3d=1}\\{{a}_{7}={a}_{1}+6d=16}\end{array}\right.$，
    解得a1=-14，d=5，
    ∴a6=a1+5d=-14+25=11．
    故答案为：11．

    点评 本题考查等差数列的第6项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

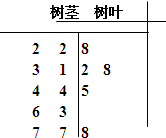
    16．在一次马拉松比赛中，35名运动员的成绩（单位：分钟）的茎叶图如图所示．若将运动员按成绩由好到差编为1～35号，再用系统抽样方法从中抽取5人，则其中成绩在区间[142，148]上的运动员人数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

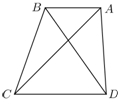    17．如图，在梯形ABCD中，AB∥CD，BC=6，cos∠ABC=-$\frac{1}{3}$．
    （Ⅰ）若∠BAC=$\frac{π}{4}$，求AC的长；
    （Ⅱ）若BD=9，求△BCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$是同一平面内的三个向量，其中$\overrightarrow a$=（-1，2）．
    （1）若|${\overrightarrow c}$|=$\sqrt{5}$，且$\overrightarrow a$∥$\overrightarrow c$，求$\overrightarrow c$的坐标；
    （2）若|${\overrightarrow b}$|=$\frac{{\sqrt{5}}}{2}$，且（$\overrightarrow a$+$\overrightarrow{2b}$）⊥（2$\overrightarrow a$-$\overrightarrow b$），求|2$\overrightarrow a$+$\overrightarrow b}$|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知p：?x0∈R，m|sinx0+2|-9≥0，q：?x∈R，x2+2mx+1，若p∨p为假命题，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=x2+|x-t|．
    （Ⅰ）当t=1时，求不等式f（x）≥1的解集；
    （Ⅱ）设函数f（x）在[0，2]上的最小值为h（t），求h（t）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．我国政府对PM 2.5采用如表标准：
    PM 2.5日均值m（微克/立方米）空气质量等级
    m＜35一级
    35≤m≤75二级
    m＞75超标
    某市环保局从一年365天的市区PM 2.5监测数据中，随机抽取10天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．
    （1）用样本数据来估计全年大概有多少天空气质量超标？
    （2）求样本数据的中位数；
    （3）从样本数据中任取2天的数据，记ξ为这2天里空气质量达到一级的天数，求ξ的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列说法中正确的个数是（　　）
    ①命题“若a=0，则ab=0”的否命题是：“若a=0，则ab≠0”；
    ②命题p：“?x∈（-∞，0），2x＜3x”，则￢p：“?x∈[0，+∞），2x≥3x”；
    ③对于实数a，b，“b＜a＜0”是“$\frac{1}{b}$＞$\frac{1}{a}$”成立的充分不必要条件
    ④如果命题“￢p”与命题“p或q”都是真命题，那么命题q一定是真命题．
    ⑤设M为平面内任意一点，则A、B、C三点共线的充要条件是存在角α，使$\overrightarrow{MB}$=sin2α•$\overrightarrow{MA}$+cos2α$\overrightarrow{MC}$．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．设a∈R，f（x）=ax2-lnx，g（x）=ex-ax．
    （1）当曲线y=f（x）在点（1，f（1））处的切线的斜率大于-1时，求f（x）的单调区间；
    （2）若f（x）•g（x）＞0对x∈（0，+∞）恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案