Question

18．我国政府对PM 2.5采用如表标准：

PM 2.5日均值m（微克/立方米）	空气质量等级
m＜35	一级
35≤m≤75	二级
m＞75	超标

某市环保局从一年365天的市区PM 2.5监测数据中，随机抽取10天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．
（1）用样本数据来估计全年大概有多少天空气质量超标？
（2）求样本数据的中位数；
（3）从样本数据中任取2天的数据，记ξ为这2天里空气质量达到一级的天数，求ξ的分布列和期望．

Answer 1

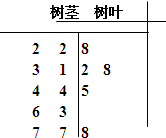
分析 （1）由表中数据及茎叶图，全年空气质量超标的大概有：365×0.2=73天，
（2）由茎叶图即可求得样本数据的中位数；
（3）确定随机变量ξ服从ξ～H（10，4，2），利用P（ξ=k）=$\frac{{C}_{4}^{k}{C}_{6}^{2-k}}{{C}_{10}^{2}}$，求解概率得出分布列及数学期望．

解答 解：（1）全年空气质量超标的大概有：365×0.2=73天，
（2）10天的中位数为$\frac{1}{2}$×（38+44）=41（微克/立方米），
（3）由ξ服从ξ～H（10，4，2），
∴P（ξ=k）=$\frac{{C}_{4}^{k}{C}_{6}^{2-k}}{{C}_{10}^{2}}$，
ξ的分布列为：

ξ	0	1	2
P	$\frac{1}{3}$	$\frac{8}{15}$	$\frac{2}{15}$

∴数学期望E（ξ）=$\frac{4×2}{10}$=$\frac{4}{5}$

点评 本题考查中位数的求法，考查离散型随机变量的分布列和数学期望的求法和应用，解题时要注意茎叶图的合理运用，充分利用样本估计总体解决，属于中档题．