
在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
(1)任意选5人;(2)甲、乙、丙三人必须参加;(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加;(5)甲、乙、丙三人至 少1人参加.
少1人参加.
解 ( 1)C
1)C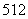 =792(种)不同的选法.
=792(种)不同的选法.
(2)甲、乙、丙三人必须参加,只需从另外的9人中选2人,共有C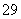 =36(种)不同的选法.
=36(种)不同的选法.
(3)甲、乙、丙三人不能参加,只需从另外的9人中选5人,共有C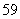 =126(种)
=126(种)
 不同的 选法.
不同的 选法.
(4)甲 、乙、丙三人只能有1人参加,分两步,先从甲、乙、丙中选1人,有C
、乙、丙三人只能有1人参加,分两步,先从甲、乙、丙中选1人,有C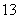 =3(种)选法,再从另外的9人中选4
=3(种)选法,再从另外的9人中选4 人有C
人有C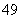 种选法,共有C
种选法,共有C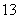 C
C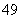 =378(种)不同
=378(种)不同 的选法.
的选法.
(5)(直接法)可分 为三类:
为三类:
第一类:甲、乙、丙中有1人参 加,共有C
加,共有C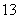 C
C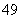 种;
种;
第二类:甲、乙、丙中有2人参加,共有C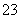 C
C 种;
种;
第三类:甲、乙、丙3人均参加,共有C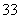 C
C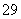 种.
种.
共有C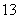 C
C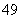 +C
+C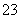 C
C +C
+C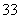 C
C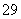 =666(种)不同的选法.
=666(种)不同的选法.


科目:高中数学 来源:2014-2015学年山东省日照市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
已知定义域为R的奇函数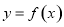 的导函数为
的导函数为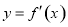 ,当
,当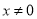 时,
时,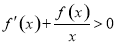 ,若
,若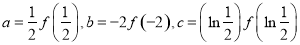 ,则
,则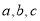 的大小关系正确的是( )
的大小关系正确的是( )
A. B.
B.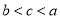 C.
C.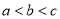 D.
D.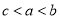
查看答案和解析>>
科目:高中数学 来源: 题型:
.第20届世界杯足球赛于2014年夏季在巴西举办,共 32支
32支 球队有幸参加,它们先分成8个小组进行循环赛,决出
球队有幸参加,它们先分成8个小组进行循环赛,决出 16强(每队均与本组其他队赛一场,各组一、二名晋级16强),这
16强(每队均与本组其他队赛一场,各组一、二名晋级16强),这
16支球队按确定的程序进行 淘汰赛,最后决出冠、亚军,此外还要决出第三名、第四名,问这届世界杯总共
淘汰赛,最后决出冠、亚军,此外还要决出第三名、第四名,问这届世界杯总共 将进行多少场比赛?
将进行多少场比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各 4张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为________.
4张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
从{-3,-2,-1,0,1,2,3}中,任取3个不同的数作为抛物线方程y=ax2+bx+c 的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条?
的系数,如果抛物线经过原点,且顶点在第一象限,则这样的抛物线共有多少条?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com