
| A�� | ���⡰��x=1����x2+x-2=0���ķ������Ǽ����� | |
| B�� | �ռ�����һ��O�벻���ߵ�����A��B��C����$\overrightarrow{OP}$=2$\overrightarrow{OA}$-2$\overrightarrow{OB}$-$\overrightarrow{OC}$����P��A��B��C�ĵ㹲�� | |
| C�� | ���⡰��x2-3x+2=0����x=1�����������Ϊ����x��1����x2-3x+2��0�� | |
| D�� | ���㣨0��2����������y2=8xֻ��һ���������ֱ����3�� |
���� ��������Ĺ�ϵ�ж�A��C�����������ߵ������ж�D�����ݸ��ݿռ��ĵ㹲��������ж�B��
��� �⣺����A�����⡰��x=1����x2+x-2=0���ķ������ǣ�����x��1����x2+x-2��0���Ǽ����⣬��A��ȷ��
����B���Կռ�����һ��O�벻���ߵ�����A��B��C����ͼ��ʾƽ�������壬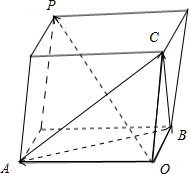
$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$����������������P��A��B��C�ĵ㲻���棬��B����
����C�����⡰��x2-3x+2=0����x=1�����������Ϊ����x��1����x2-3x+2��0������C��ȷ��
����D�����㣨0��2����������y2=8xֻ��һ���������ֱ����3����
��ͼʾ��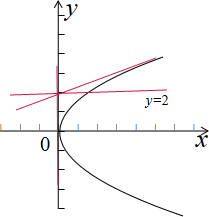 ��
��
һ�����ߣ�һ����y=2��һ����x=0����D��ȷ��
��ѡ��B��
���� ������Ҫ�������������жϣ�Ҫ�����������������йظ������ѧ���������ж����������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
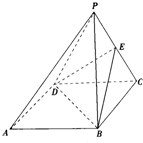 ��֪����P-ABCD�У������ı���Ϊ�����Σ�����PDCΪ�������Σ���ƽ��PDC�͵���ABCD��EΪPC���е�
��֪����P-ABCD�У������ı���Ϊ�����Σ�����PDCΪ�������Σ���ƽ��PDC�͵���ABCD��EΪPC���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m��n��n�ͦ£�m?��������ͦ� | B�� | �����ͦã��¡ͦã����ɦ�=l����l�ͦ� | ||
| C�� | �����ͦ£�a?������a�ͦ� | D�� | �����ͦ£�a�ɦ�=AB��a�Φ���a��AB����a�ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com