设f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝2x.若对任意的x∈[a，a＋2]，不等式f(x＋a)≥f2(x)恒成立，则实数a的取值范围是________．
黄冈天天练口算题卡系列答案科目：高中数学 来源： 题型：
设P是不等式组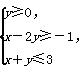
表示的平面区域内的任意一点，向量m＝(1,1)，n＝(2,1)，若
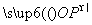＝λm＋μn(λ，μ∈R)，则μ的最大值为( )
A．3 B.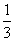
C．0 D．－1
查看答案和解析>>
科目：高中数学 来源： 题型：
在三棱柱ABC－A1B1C1中，侧面ABB1A1为矩形，AB＝1，AA1＝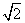
，D为AA1的中点，BD与AB1交于点O，CO⊥侧面ABB1A1.
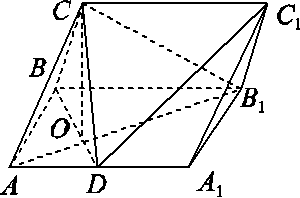
(1)证明：BC⊥AB1；
(2)若OC＝OA，求三棱锥C1－ABC的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
若函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上是单调递增函数．如果实数t满足f(ln t)＋f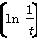
≤2f(1)，那么t的取值范围是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知f(x)＝2x2＋px＋q，g(x)＝x＋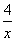
是定义在集合M＝
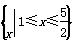上的两个函数．对任意的x∈M，存在常数x0∈M，使得f(x)≥f(x0)，g(x)≥g(x0)，且f(x0)＝g(x0)．则函数f(x)在集合M上的最大值为( )
A.
B．4
C．6 D.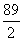
查看答案和解析>>
科目：高中数学 来源： 题型：
节能灯的质量通过其正常使用时间来衡量，使用时间越长，表明质量越好，且使用时间大于或等于6千小时的产品为优质品．现用A，B两种不同型号的节能灯做试验，各随机抽取部分产品作为样本，得到试验结果的频率分布直方图如图所示．
以上述试验结果中使用时间落入各组的频率作为相应的概率．
(1)现从大量的A，B两种型号节能灯中各随机抽取两件产品，求恰有两件是优质品的概率；
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”．通过多年统计发现，A型节能灯每件产品的利润y(单位：元)与其使用时间t(单位：千小时)的关系如下表：
| 使用时间t (单位：千小时) | t<4 | 4≤t<6 | t≥6 |
| 每件产品的 利润y(单位：元) | －20 | 20 | 40 |
若从大量的A型节能灯中随机抽取两件，其利润之和记为X(单位：元)，求X的分布列及数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
[解析] 由题意知，f(x)＝2|x|，所以f(x＋a)≥f2(x)等价于2|x＋a|≥2|2x|，等价于|x＋a|≥|2x|，平方得3x2－2ax－a2≤0，即(x－a)(3x＋a)≤0在x∈[a，a＋2]上恒成立，等价于[a，a＋2]是
的一个子区间．
，a]的一个子区间，所以a>0不合题意．
的一个子区间
解得a≤－
.
若存在k使得函数f(x)的值域是[0,2]，则实数a的取值范围是( )
，＋∞) B.
ln(1－x)的定义域是( )
的图象可能是( )
