
分析 (1)若a=1,则函数f(x)=$\frac{1-{3}^{x}}{1+{3}^{x+1}}$,f(-x)≠-f(x),进而得到结论;
(2)若此函数是奇函数,则a=3,
①结合指数函数的单调性,和单调性的性质,可判断函数f(x)为减函数,利用定义法,可证得结论;
②结合函数的单调性和奇偶性,可将不等式化为m(log3x)2+1<m(log3x)+2恒成立,令t=log3x,则mt2+1<mt+2恒成立,则mt2-mt-1<0恒成立,再由二次函数的图象和性质,得到m的范围.
解答 证明:(1)若a=1,则函数f(x)=$\frac{1-{3}^{x}}{1+{3}^{x+1}}$.
此时f(-x)=$\frac{1-{3}^{-x}}{1+{3}^{-x+1}}$=$\frac{{3}^{x}-3}{3+{3}^{x}}$,
-f(x)=-$\frac{1-{3}^{x}}{1+{3}^{x+1}}$,
f(-x)≠-f(x),
故函数f(x)不是奇函数;
(2)①若此函数是奇函数,则f(-x)=-f(x),
故$\frac{1-{3}^{-x}}{a+{3}^{-x+1}}$=$\frac{{3}^{x}-1}{a•{3}^{x}+{3}^{\;}}$=-$\frac{1-{3}^{x}}{a+{3}^{x+1}}$=$\frac{{3}^{x}-1}{a+{3}^{x+1}}$,
故a•3x+3=a+3x+1,
解得:a=3,
此时f(x)=$\frac{1-{3}^{x}}{3+{3}^{x+1}}$=$-\frac{1}{3}$+$\frac{2}{3+{3}^{x+1}}$,
此时函数f(x)为减函数,
理由如下:
∵$3+{3}^{{x}_{1}+1}>0$,$3+{3}^{{x}_{2}+1}>0$,${3}^{{x}_{2}+1}-{3}^{{x}_{1}+1}>0$,
∴f(x1)-f(x2)=($-\frac{1}{3}$+$\frac{2}{3+{3}^{{x}_{1}+1}}$)-($-\frac{1}{3}$+$\frac{2}{3+{3}^{{x}_{2}+1}}$)=$\frac{2}{3+{3}^{{x}_{1}+1}}$-$\frac{2}{3+{3}^{{x}_{2}+1}}$=$\frac{2({3}^{{x}_{2}+1}-{3}^{{x}_{1}+1})}{(3+{3}^{{x}_{1}+1})(3+{3}^{{x}_{2}+1})}$>0,
故函数f(x)为减函数,
②若f[m(log3x)2+1]+f[-m(log3x)-2]>0恒成立,
则f[m(log3x)2+1]>-f[-m(log3x)-2]恒成立,
则f[m(log3x)2+1]>f[m(log3x)+2]恒成立,
则m(log3x)2+1<m(log3x)+2恒成立,
令t=log3x,则mt2+1<mt+2恒成立,
则mt2-mt-1<0恒成立,
当m=0时,满足条件,
当m≠0时,$\left\{\begin{array}{l}m<0\\△={m}^{2}+4m<0\end{array}\right.$,解得:-4<m<0,
综上所述:m∈(-4,0].
点评 本题考查的知识点是函数的单调性,函数的奇偶性,恒成立问题,二次函数的图象和性质,指数函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
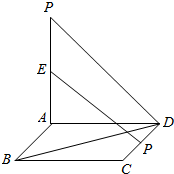 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com