
(本小题满分12分)已知函数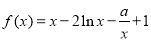 ,
,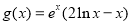 .
.
(Ⅰ)若函数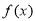 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围;
(Ⅱ)求 的最大值.
的最大值.
(1)[1,+∞);(2)-e.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值等基础知识,意在考查考生的分析问题解决问题的能力、转化能力、运算求解能力.第一问,先对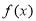 求导,将函数
求导,将函数 在定义域上是增函数,转化为
在定义域上是增函数,转化为 恒成立,即转化为
恒成立,即转化为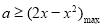 ,配方法得到
,配方法得到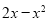 的最大值,即可得到a的取值范围;第二问,先对
的最大值,即可得到a的取值范围;第二问,先对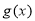 求导,结合第一问的结论,知
求导,结合第一问的结论,知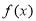 在定义域上是增函数,且
在定义域上是增函数,且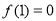 ,利用
,利用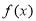 的单调性,得到
的单调性,得到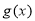 的单调性,从而知当
的单调性,从而知当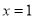 时
时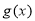 取得最大值.
取得最大值.
试题解析:(Ⅰ)由题意得x>0,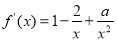 . 1分
. 1分
由函数f(x)在定义域上是增函数得,f(x)≥0,即a≥2x-x2=-(x-1)2+1(x>0).
因为-(x-1)2+1≤1(当x=1时,取等号),
所以a的取值范围是[1,+∞). 5分
(Ⅱ)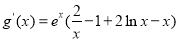 , 7分
, 7分
由(Ⅰ)得a=2时,f(x)=x-2lnx-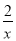 +1
+1
且f(x)在定义域上是增函数得,又f(1)=0,
所以,当x∈(0,1)时,f(x)<0,当x∈(1,+∞)时,f(x)>0. 10分
所以,当x∈(0,1)时,g(x)>0,当x∈(1,+∞)时,g(x)<0.
故x=1时,g(x)取得最大值-e. 12分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值.
考点分析: 考点1:导数及其应用 试题属性

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年陕西省宝鸡市九校高三联合检测理科数学试卷(解析版) 题型:解答题
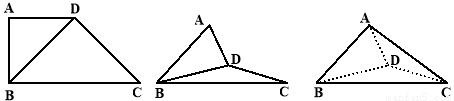
在梯形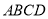 中,
中, ,
,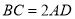 ,
,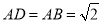 ,
,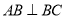 ,如图把
,如图把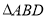 沿
沿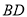 翻折,使得平面
翻折,使得平面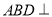 平面
平面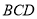 .
.
(Ⅰ)求证: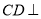 平面
平面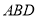 ;
;
(Ⅱ)若点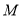 为线段
为线段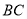 中点,求点
中点,求点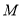 到平面
到平面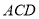 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:选择题
在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注数字外完全相同,现从中随机取2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.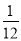 B.
B.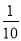 C.
C.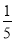 D.
D.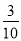
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试理科数学试卷(解析版) 题型:选择题
已知不等式组 ,表示的平面区域为M,若直线
,表示的平面区域为M,若直线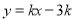 与平面区域M有公共点,则k的取值范围是( )
与平面区域M有公共点,则k的取值范围是( )
A. 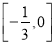 B.
B. 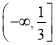 C.
C. 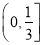 D.
D. 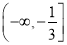
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试文科数学试卷(解析版) 题型:填空题
在半径为2的球面上有不同的四点A、B、C、D,若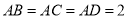 ,则平面BCD被球所截面图形的面积为 .
,则平面BCD被球所截面图形的面积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三上学期阶段性考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在平面直角坐标系中,点 在角
在角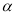 的终边上,点
的终边上,点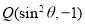 在角
在角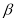 的终边上,且
的终边上,且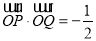 .
.
(1)求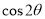 的值;(2)求
的值;(2)求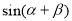 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com