设函数
（1）解不等式
；
（2）求函数
的最小值.
（1）
；（2）
.
【解析】
试题分析：（1）解含绝对值的不等式，关键是去掉绝对值符号，其方法有三种：①定义法；②平方法；③分区间讨论法，这里用的是分区间讨论法，遇到多个绝对值时常用此方法；（2）求绝对值函数的值域，通常是通过分区间讨论，去掉绝对值符号，将绝对值函数改写成分段函数，然后就每段求
的范围，最后再将每段求得的范围求并集，注意不是求交集，从而得到绝对值函数的值域.
试题解析：（1）不等式
等价于：
①
；
②
；
③
，
综合①②③得不等式的解集为： 5分
（2）①当
时，
；
②当
时，
③当
时，
综合①②③得函数
的值域为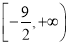
，因此求函数的最小值为. 10分
考点：1.含绝对值的不等式的解法；2.绝对值函数的值域的求法；3.分类讨论思想.
课堂全解字词句段篇章系列答案科目：高中数学 来源：2015届四川成都树德中学高二3月月考文科数学试卷（解析版） 题型：选择题
命题
； 命题
，双曲线
的离心率为
，则下面结论正确的是（ ）
A．
是假命题 B．
是真命题 C．
是假命题 D．
是真命题
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期末考试理科数学试卷（解析版） 题型：选择题
已知函数
的两个极值点分别为
，且
，点
表示的平面区域为
，若函数
（
）的图象上存在区域
内的点，则实数
的取值范围是（ ）
A.
B.
C.
D.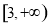
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期末考试文科数学试卷（解析版） 题型：解答题
某校高三年级有男学生105人，女学生126人，教师42人，用分层抽样的方法从中抽取13人进行问卷调查，设其中某项问题的选择，分别为“同意”、“不同意”两种，且每人都做了一种选择，下面表格中提供了被调查人答卷情况的部分信息．
| 同意 | 不同意 | 合计 |
教师 | 1 |
|
|
女学生 |
| 4 |
|
男学生 |
| 2 |
|
（1）完成此统计表；（2分）
（2）估计高三年级学生“同意”的人数；（4分）
（3）从被调查的女学生中选取2人进行访谈，求选到两名学生中恰有一人“同意”，一人“不同意”的概率．（6分）
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期末考试文科数学试卷（解析版） 题型：选择题
已知抛物线
（
）的焦点
为双曲线
（
）的一个焦点，经过两曲线交点的直线恰过点
，则该双曲线的离心率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期中考试理科数学试卷（解析版） 题型：解答题
为了解某班关注NBA（美国职业篮球）是否与性别有关，对某班48人进行了问卷调查得到如下的列联表：
| 关注NBA | 不关注NBA | 合计 |
男生 |
| 6 |
|
女生 | 10 |
|
|
合计 |
|
| 48 |
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为
.
（1）请将上面的表补充完整（不用写计算过程），并判断是否有95%的把握认为关注NBA与性别有关？说明你的理由；
（2）设甲，乙是不关注NBA的6名男生中的两人，丙，丁，戊是关注NBA的10名女生中的3人，从这5人中选取2人进行调查，求：甲，乙至少有一人被选中的概率.
答题参考
P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中数学 来源：2015届吉林省高二下学期期中考试理科数学试卷（解析版） 题型：解答题
如图，点
为斜三棱柱
的侧棱
上一点，
交
于点
，
交
于点
.
(1) 求证：
；
(2) 在任意
中有余弦定理：
.
拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则
（ ）
B.
C.
D.
的内角
所对边的长分别为
，若
，
，则角
（ ）
B.
C.
D.