练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．直线$\left\{\begin{array}{l}{x=sinθ+tsin15°}\\{y=cosθ-tsin15°}\end{array}\right.$（t为参数，θ是常数）的倾斜角是（　　）
    A．45°B．75°C．105°D．135°

    分析 消去参数t，得到直线的普通方程，然后求解直线的倾斜角．

    解答 解：直线$\left\{\begin{array}{l}{x=sinθ+tsin15°}\\{y=cosθ-tsin15°}\end{array}\right.$（t为参数，θ是常数）消去参数t，可得：x+y=sinθ+cosθ．
    直线的斜率为：-1．
    直线$\left\{\begin{array}{l}{x=sinθ+tsin15°}\\{y=cosθ-tsin15°}\end{array}\right.$（t为参数，θ是常数）的倾斜角是：135°．
    故选：D．

    点评 本题考查直线的参数方程与普通方程的互化，直线的倾斜角的求法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．数列{an}满足：a1=$\frac{1}{2}$，an+1=an+$\frac{1}{{4n}^{2}-1}$，则实数{an}的通项公式为an=$\frac{4n-3}{2（2n-1）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知函数f（x）=2015sinx+x2015+2015tanx+2015，且f（-2015）=2016，则f（2015）的值为2014．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

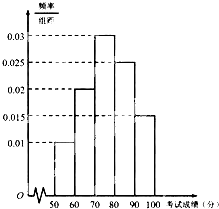    7．某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．
    （1）试估计全市学生参加汉字听写考试的平均成绩；
    （2）如果从参加本次考试的同学中随机选取1名同学，求这名同学考试成绩在80分以上的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数y=4b2-3b2sin2θ-3bsinθ+$\frac{9}{4}$的最大值为7，求实数b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=（a-1）lnx+ax2+1．
    （1）讨论函数f（x）的单调性；
    （2）如果对任意的x1＞x2＞0，总有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$≥2，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设A，B为两个事件，已知P（A）=$\frac{2}{3}$，P（AB）=$\frac{1}{3}$，则P（B|A）=（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{2}{9}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．函数f（x）的二次项系数为a，且f（x）＞-2x的解集是（1，3）．若f（x）+6a=0有两个等根，求f（x）解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下列判断正确的是（　　）
    A．函数$f（x）=\frac{{{x^2}-x}}{x-1}$是奇函数
    B．函数$f（x）=（1-x）\sqrt{\frac{1+x}{1-x}}$是偶函数
    C．函数$y=\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$是偶函数
    D．函数$y=\frac{{\sqrt{9-{x^2}}}}{{|{x+4}|+|{x+3}|}}$的图象关于y轴对称

    查看答案和解析>>

    同步练习册答案