【题目】在平面直角坐标系
中，椭圆
的离心率为
，过椭圆右焦点
作两条互相垂直的弦
与
.当直线的斜率为0时，
.
（1）求椭圆的方程；
（2）试探究
是否为定值？若是，证明你的结论；若不是，请说明理由.
【答案】（1）
（2）
是定值；证明见解析
【解析】
（1）根据
，当直线
的斜率为0时，
.即
求解.
（2）分两种情况讨论，①当两条弦中一条弦所在直线的斜率为0时，另一条弦所在直线的斜率不存在，易得
.
②当两弦所在直线的斜率均存在且不为0时，设直线的方程为
，直线
的方程为
.将直线方程代入椭圆方程中并整理
，再利用弦长公式分别求解
即可.
（1）由题意知，当直线的斜率为0时，.
.
又
，
解得
，
，
所以椭圆方程为.
（2）①当两条弦中一条弦所在直线的斜率为0时，另一条弦所在直线的斜率不存在，
由题意知.
②当两弦所在直线的斜率均存在且不为0时，设直线的方程为，
，
，
则直线的方程为.
将直线方程代入椭圆方程中并整理得，
则
，
，
所以
.
同理，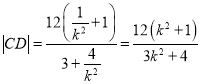
.
所以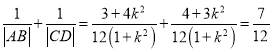
，
故是定值.
科目：高中数学 来源： 题型：
【题目】已知椭圆：
的四个顶点围成的四边形的面积为
，原点到直线
的距离为
.
（1）求椭圆
的方程；
（2）已知定点
，是否存在过
的直线
，使与椭圆交于
，
两点，且以
为直径的圆过椭圆的左顶点？若存在，求出的方程：若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了提高利润，从2012年至2018年每年对生产环节的改进进行投资，投资金额与年利润增长的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
（1）请用最小二乘法求出
关于
的回归直线方程（结果保留两位小数）；
（2）现从2012—2018年这7年中抽出三年进行调查，记
年利润增长－投资金额，设这三年中
（万元）的年份数为
，求随机变量的分布列与期望.
参考公式：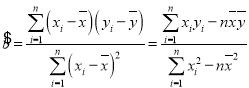
，
.
参考数据：
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，长途车站P与地铁站O的距离为
千米，从地铁站O出发有两条道路l1，l2，经测量，l1，l2的夹角为45°，OP与l1的夹角
满足tan＝
（其中0＜θ＜
)，现要经过P修条直路分别与道路l1，l2交汇于A，B两点，并在A，B处设立公共自行车停放点．
（1）已知修建道路PA，PB的单位造价分别为2m元/千米和m元/千米，若两段道路的总造价相等，求此时点A，B之间的距离；
（2）考虑环境因素，需要对OA，OB段道路进行翻修，OA，OB段的翻修单价分别为n元/千米和
n元/千米，要使两段道路的翻修总价最少，试确定A，B点的位置．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C的方程为：（x－3）2＋（y－2）2＝r2（r>0），若直线3x＋y＝3上存在一点P，在圆C上总存在不同的两点M，N，使得点M是线段PN的中点，则圆C的半径r的取值范围是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的中心为坐标原点，焦点在
轴上，离心率
，以椭圆的长轴和短轴为对角线的四边形的周长为
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若经过点
的直线
交椭圆于
两点，是否存在直线
，使得到直线
的距离
满足
恒成立，若存在，请求出
的值；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
